4.3.1.1 模型描述
对于三阶段的离散型估值分布的研究, 我们依然参考Hu 等(2015), 分数量型策略、 利润型策略、 跨期定价策略、 菜单定价策略四种情况进行讨论。 与两阶段模型不同的是, 三阶段模型中第二阶段的潜在支持者B2 既要观察B1 的决策, 又要推测第三阶段的潜在支持者B3 的策略, 决策过程更加复杂。
针对三阶段的模型, 我们有如下假设:
①潜在支持者B1、 B2、 B3 的估值分布服从两点分布: 高估值H 和低估值L,其概率分别为α 和1 -α。
②若众筹项目第一阶段或第二阶段的潜在支持者进行了投资, 但最终众筹项目失败, 则项目发起方获得的筹资额为βPi(i=1,2) (Pi 为发起方在第i 阶段设定的投资额)。
下面我们将分别对四种不同的定价策略下发起方的最优决策进行讨论。
4.3.1.2 数量型策略
与两阶段模型类似, 项目发起方在三个阶段设定的价格皆为低估值L, 即(L, L, L), 而项目的筹资目标为T=3L。 显然, 三个潜在支持者B1、 B2、 B3 的估值都不小于L。 所以, 众筹项目必然成功, 即项目成功概率s =1, 而发起人的期望收益为π =3L。
4.3.1.3 利润型策略
与两阶段模型类似, 项目发起方在三个阶段的定价皆为高估值H, 即(H,H, H), 所以, 众筹的筹资目标为T=3H。
对B1 来说, 当估值是L 时, 一定不会投资, 项目必然失败。 而当其估值是H 时, 若B2、 B3 的估值同时都为H, 则项目会成功, B1 的效用为H -H =0; 否则, 项目会失败, B1 的效用是-βH。 所以, 此时B1 的期望效用为:
E1 =α2(H-H) +( -βH)(1 -α2) =(α2 -1)βH
由于α∈[0, 1], 所以E1 ≤0。 当且仅当β =0 时, E1 =0, B1 才会选择投资, 项目才可能成功; 否则, β >0 时, B1 不会投资, 项目必然失败。
综上所述, 在利润型策略下, 众筹项目成功需满足的条件是β =0 且三个阶段B1、 B2、 B3 的估值都是H。 所以, 项目发起方应采用AON 机制。 此时, 项目成功的概率为s=α3, 项目发起方的期望收益为π =3α3H。
4.3.1.4 跨期定价策略
与两阶段模型类似, 在跨期定价策略下, 项目发起方在每个阶段的定价都可以是高估值H 或者低估值L。 考虑三个阶段发起方可以选择不同的价格, 那么一共可以有6 种不同的定价方式, 分别是(H, H, L), (H, L, H), (H, L, L),(L, H, H), (L, H, L) 和(L, L, H)。 而每个潜在支持者的估值有H 和L 两种, 那么, 三个阶段的潜在支持者的估值分布总共会有8 种情形。 为了分析不同定价情况下, 项目发起方的期望收益以及最优定价策略, 以找出最优的一种跨期定价方式, 需要讨论每一种定价时三个阶段支持者的投资决策。 表4.4 给出了在不同定价方式下, 支持者具有不同估值时, 参与众筹项目所获得的效用。
表4.4 六种跨期型定价方式下支持者的效用
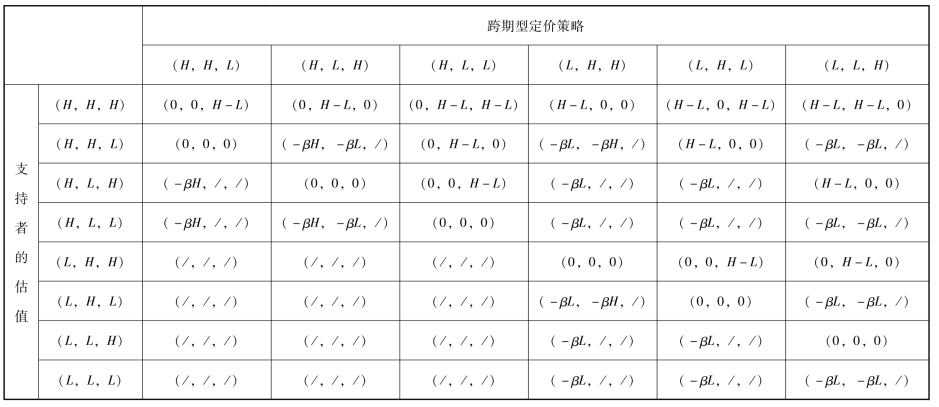
下面我们对不同的定价方式进行具体分析。
①当定价为(H, H, L) 时:
·若B1 的估值是L, 则一定不会投资, 项目必然失败, 项目发起方的收益π=0。
·若B1 的估值是H, 当β=0 时, 容易得到, B1 的期望效用E1 =0。 所以,B1 愿意投资。 当B2 的估值是H 时, 项目会成功, 因此, 项目成功的概率为s=α2, 发起方的期望收益为π=α2(2H+L)。 当β >0 时, 容易得到, B1 的期望效用E1 = -βH(1 -α) <0, 所以, B1 不会投资, 项目必然失败。
综上所述, 定价为(H, H, L) 时, 若β=0, 项目发起方的期望收益为π=α2(2H+L); 若β >0, 发起方的期望收益π =0。 所以, 此种定价方式下, 项目发起方应采用AON 机制。
②定价为(H, L, H) 和(H, L, L) 的情形与定价为(H, H, L) 的分析过程类似, 这里不再赘述。 相关结论如下:
·当定价为(H, L, H) 时, 若β =0, 项目发起方的期望收益为π = α2(2H+L); 若β >0, 发起方的期望收益为π=0。
·当定价为(H, L, L) 时, 若β =0, 项目发起方的期望收益为π = α(H+2L); 若β >0, 发起方的期望收益为π=0。
很显然, 在这两种定价方式下, 项目发起方仍然应采用AON 机制。
③当定价为(L, H, L) 时:
·若B1 的估值是L, 当β =0 时, 容易得到, B1 的期望效用E1 =0, 所以,B1 会选择投资。 当B2 的估值是H 时, 可以得到, 其期望效用E2 =0, 所以, B2也会选择投资。 此时, 项目的成功率为s =(1 -α)α, 项目发起方的期望收益为π=α(1 -α)(H+2L)。 当β >0 时, 容易得到, B1 的期望效用E1 =α(L-L) -βL(1 -α) = -βL(1 -α) <0, 所以, B1 不会投资, 项目必然失败, 项目发起方的期望收益为π=0。
·若B1 的估值是H, 当β=0 时, B1 的期望收益E1 =α(H -L) >0, 所以,B1 会选择投资。 当B2 的估值是H 时, 可以得到, 其期望效用E2 =0, 所以, B2也会选择投资。 此时, 项目的成功率为s =α2, 项目发起人的期望收益为π =α2(H+2L)。 当β >0 时, 容易得到, B1 的期望效用为E1 =α(H -L) -βL(1 -α)。而对项目发起方来说, 若B1 和B2 都进行投资, 则项目成功, 其概率为s =α2;若只有B1 进行投资, 则项目失败, 但发起方能够保留一部分筹资额, 这种情况的概率为α(1 -α)。 所以, 项目发起方的期望收益为:
![]()
显然, β 越大, 发起方的期望收益越高。 结合条件E1≥0, 可以得到:
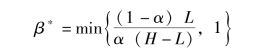
分析该结果, 可以得到, 当αH >L 时,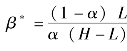 。 此时, 项目发起方的期望收益为:
。 此时, 项目发起方的期望收益为: 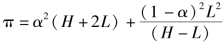 。 当αH≤L 时, β =1, 项目发起方的期望收益为π=α2(H+L) +αL。
。 当αH≤L 时, β =1, 项目发起方的期望收益为π=α2(H+L) +αL。
综上所述, 可以得到, 当定价为(L, H, L) 时, 若β=0, 项目发起方的期望收益为π=α(H+2L)。 若β >0, 则当αH >L 时, 应有![]() , 发起方的期望收益为
, 发起方的期望收益为![]() ; 当αH≤L 时, β =1, 发起方的期望收益为π=α2(H+L) +αL。
; 当αH≤L 时, β =1, 发起方的期望收益为π=α2(H+L) +αL。
比较上述结果, 可以发现, β =0 时, 项目发起方的期望收益最大。 因此,当定价为(L, H, L) 时, 发起方仍然应该采用AON 机制。
④当定价为(L, H, H) 和(L, L, H) 时, 分析过程与③类似, 这里不再赘述。
相关结论为: 当定价为(L, H, H) 时, 若β =0, 则项目发起方的期望收益为π=α2 (2H+L); 若β >0, 则发起方的期望收益π =0。 当定价为(L, L,H) 时, 若β=0, 则项目发起方的期望收益为π=α(H+2L)。 若β >0, 则当α2 >![]() 时, β =1, 项目发起方的期望收益为π =α3(2L +H) +α(1 -α)(1 +2α)L;当
时, β =1, 项目发起方的期望收益为π =α3(2L +H) +α(1 -α)(1 +2α)L;当![]() 时,
时,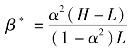 , 发起方的期望收益π =α3(2L +H) +α3(1 -α)
, 发起方的期望收益π =α3(2L +H) +α3(1 -α)![]() 。 比较这两种定价方式下项目发起方的期望收益, 可以发现, β =0 时, 其期望收益更高, 所以, 项目发起方仍应采用AON 机制。
。 比较这两种定价方式下项目发起方的期望收益, 可以发现, β =0 时, 其期望收益更高, 所以, 项目发起方仍应采用AON 机制。
如表4.5 所示总结了在六种不同的定价方式下, 项目发起方采用不同机制时的期望收益。 我们可以得到如下定理:
表4.5 六种定价方式下项目发起方采用不同机制时的期望收益
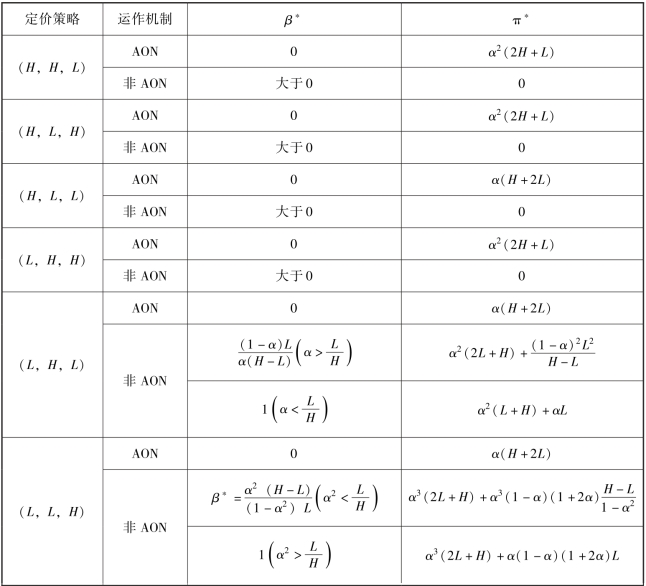
定理4.3 在三阶段奖励型众筹中, 若项目发起方选择跨期定价策略, 则:
①项目发起方应采用AON 机制。
②当![]() 时, 项目发起方的最优定价为(H, L, L), (L, H, L) 或(L, L, H); 当
时, 项目发起方的最优定价为(H, L, L), (L, H, L) 或(L, L, H); 当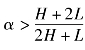 时, 最优定价为(H, H, L), (H, L, H) 或(L,H, H)。
时, 最优定价为(H, H, L), (H, L, H) 或(L,H, H)。
从上述定理中, 我们可以发现, 当α 较大时(即潜在支持者有较大的可能性具有高估值时), 项目发起方可以在任意两个阶段选择高估值作为支持金额; 反之, 则项目发起方只能在一个阶段选择高估值作为支持金额。
4.3.1.5 菜单定价策略
与两阶段模型类似, 我们假设项目发起方仍然提供两种可选择的菜单价格Ph 和Pl, 满足Pl≤L≤Ph≤H。 需要注意的是, 在三阶段奖励型众筹模型中, 项目发起方有两种筹资目标设定方式, 即筹资目标T 分别为2Ph +Pl 和2Pl +Ph。下面我们将分别讨论这两种不同的情况。
(1) 筹资目标T=2Ph +Pl
此时, 分析过程与两阶段模型类似, 但更为复杂。 很显然, 每一个潜在支持者都会计算自己的期望效用, 然后再做出决策。 对B3 来说, 前两个支持者的决策已经确定, 他只需要根据自己的估值做出理性的决策; 而B2 在做决策时, 可以观察到B1 的决策, 同时要对B3 的决策做一预期; 而B1 则仅知晓自己的估值,需要分析B2 和B3 的可能决策, 所以, 其决策最为复杂。
因此, 我们的分析主要围绕B1 展开。 假设他的估值为H, 我们可以绘制出如图4.2 所示的决策树以帮助分析其决策过程。 而B1 的估值为L 时, 其分析过程类似, 省略相应的决策树示意图。
另外, 在三阶段模型之下, 我们依然采用机制设计的思路, 使得在项目有可能成功的情况下, 高估值的支持者愿意出高价, 而低估值的支持者愿意出低价。
结合图4.2, 我们首先分析B3 的决策。 对B3 来说, 如果其估值为L, 且项目恰好只差Pl 即可成功, 那么, B3 必然会投资Pl; 若差Ph 成功, 项目将会失败。 如果B3 的估值是H, 前两阶段至少要有一个潜在支持者投资Ph, 则项目会成功; 否则, 项目将会失败。 其中, 若前两阶段潜在支持者的投资均为Ph, 则B3 将投资Pl。
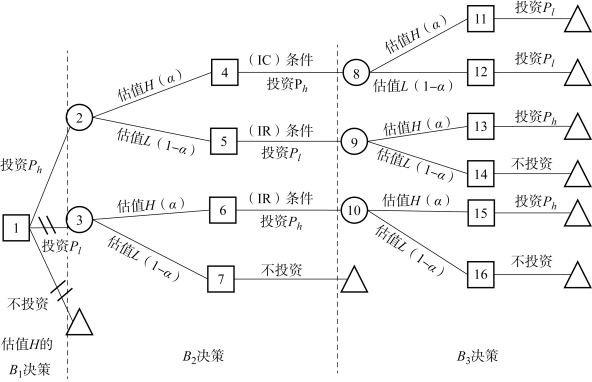
图4.2 三阶段菜单型定价策略决策树示意图(T=2Ph +Pl)
对B2 来说, 如果其估值为H, 同时若观察到B1 投资Ph, 则B2 可能投资Ph也可能投资Pl。 为了最大化项目成功的可能性, 项目发起方应设置激励相容条件(4.15) 式, 使得B2 的估值为H 时将投资Ph; 若B2 观察到B1 投资Pl, 要使得B2 愿意参与到众筹项目中, 则应满足条件(4.16) 式。 而B2 的估值为L 时, 若观察到B1 投资Ph, 则要保证B2 参与到众筹中, 应满足条件(4.17) 式; 若观察到B1 投资Pl, 则项目肯定无法成功, 所以, B2 不会投资。
对B1 来说, 如果其估值为H, 为了激励他投资高价, 需满足当他出高价时所获得的期望效用大于等于其投资低价的期望效用, 所以应设置条件(4.18)式; 若B1 的估值是L, 则应保证其愿意投资Pl 而不是放弃参与众筹, 因此, 需满足约束条件(4.19) 式。
此外, 我们可以得到不同情形下项目发起方的期望收益, 从而构建出如下所示的优化问题:
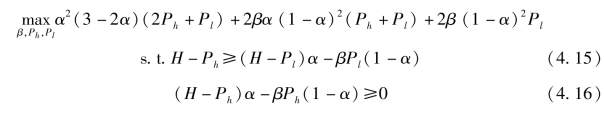
 (https://www.daowen.com)
(https://www.daowen.com)
其中, β、 Ph 和Pl 是决策变量。
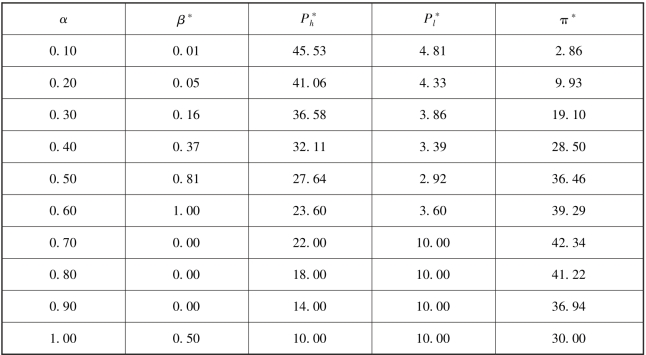
由于上述模型较为复杂, 难以直接求得决策变量的显示解。 所以, 我们通过一个数值算例来进行分析。 假设H =50, L =10, 考虑潜在支持者具有高估值的概率α 从0 到1 变化, 我们可以得到如表4.6 和图4.3 所示的结果。
表4.6 菜单定价策略下高估值概率变化时的结果(T=2Ph +Pl)
观察上述结果, 我们可以得到:
结论4.1 在三阶段模型中, 当菜单定价策略的众筹目标为T =2Ph +Pl 时,AON 机制不一定是项目发起方应采用的最优机制。 在不同的α 下, β也会发生变化。
·当α≤0.65 时, β递增,  单调递减, π单调递增。
单调递减, π单调递增。
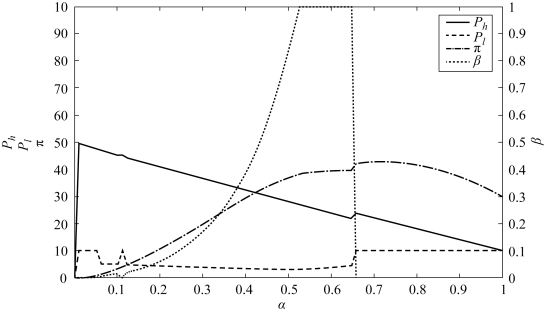
图4.3 菜单定价策略下不同高估值概率的结果(T=2Ph +Pl)
·当α >0.65 时, β =0 (注意: α=1 时, β =0.5 没有实际意义, 因为项目一定会成功),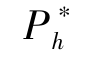 单调递减, π先增后减。
单调递减, π先增后减。
显然, 当α 很小时, 潜在支持者具有高估值的可能性很小, 所以, 众筹项目很难成功。 此时, 把β设置的低一些可以减少潜在支持者的顾虑。 同时, 把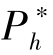 和
和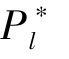 定得高一些, 是为了保证一旦有高估值的潜在投资者到达, 项目发起方可以获得较高的收益。 当α 逐渐增大, 具有高估值的潜在支持者到达的概率提高,所以, 发起方可以考虑增加β 以在项目失败时保留尽可能多的已筹资金。 因此,项目发起方会逐渐降低
定得高一些, 是为了保证一旦有高估值的潜在投资者到达, 项目发起方可以获得较高的收益。 当α 逐渐增大, 具有高估值的潜在支持者到达的概率提高,所以, 发起方可以考虑增加β 以在项目失败时保留尽可能多的已筹资金。 因此,项目发起方会逐渐降低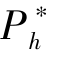 和
和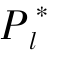 , 以更好地吸引潜在支持者参与到众筹项目中。而随着α 的不断提高, 项目成功的概率也随之增加。 对项目发起方来说, 此时选择增加项目成功的可能性会是更加合理的选择。 所以, 当α 足够大之后, 高估值的支持者出现的概率占到一多半时, 项目的成功率是很大的, 此时宜采取“以促进项目成功为主” 的定价策略, 具体措施就是取β =0。 这意味着发起方应采用AON 机制, 这将打消潜在支持者对项目失败产生损失的顾虑。 所以, 我们发现此时
, 以更好地吸引潜在支持者参与到众筹项目中。而随着α 的不断提高, 项目成功的概率也随之增加。 对项目发起方来说, 此时选择增加项目成功的可能性会是更加合理的选择。 所以, 当α 足够大之后, 高估值的支持者出现的概率占到一多半时, 项目的成功率是很大的, 此时宜采取“以促进项目成功为主” 的定价策略, 具体措施就是取β =0。 这意味着发起方应采用AON 机制, 这将打消潜在支持者对项目失败产生损失的顾虑。 所以, 我们发现此时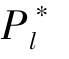 =L。 而且, 为了激励具有高估值的潜在支持者选择高价格, 需满足条件H-Ph≥α (H-L)。 那么, 当α 增加时,
=L。 而且, 为了激励具有高估值的潜在支持者选择高价格, 需满足条件H-Ph≥α (H-L)。 那么, 当α 增加时, 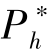 必然随之降低。 最终, 当α =1 时,
必然随之降低。 最终, 当α =1 时,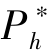 =L。 随着α 逐渐接近于1, 潜在支持者具有高估值的可能性越来越大, 项目成功的概率也越来越大, β的取值便逐渐失去了意义。
=L。 随着α 逐渐接近于1, 潜在支持者具有高估值的可能性越来越大, 项目成功的概率也越来越大, β的取值便逐渐失去了意义。
(2) 筹资目标T=2Pl +Ph
当筹资目标为T =2Pl +Ph 时, 分析过程与情况(1) 类似。 图4.4 描述了B1 的估值为H 时的决策树。 这里, 我们同样忽略B1 的估值为L 时的决策树。
结合图4.4 所示的三阶段菜单型定价策略决策树示意图, 可以知道, 对B3来说, 如果其估值为H, 那么, 项目必然可以成功。 因为无论距离筹资目标差Ph还是Pl, B3 都愿意补上最后的资金缺口。 如果B3 的估值是L, 若距离筹资目标还差Ph, 则B3 不会参与众筹项目; 若只差Pl, 则B3 会投资Pl 促使项目成功。

图4.4 三阶段菜单型定价策略决策树示意图(T=2Pl +Ph)
对B2 来说, 如果其估值为H, 若观察到B1 的投资为Ph, 则B2 一定会选择投资Pl; 若观察到B1 的投资为Pl, 则项目发起方为了保证众筹成功率, 应使得B2 选择投资Ph, 其条件为(4.20) 式。 当B2 的估值是L 时, 若观察到B1 的投资为Ph, B2 一定会选择投资Pl; 若观察到B1 的投资为Pl, 则需保证(4.21)式成立, B2 才会投资Pl。
最后, 对B1 来说, 如果其估值为H, 项目发起方为了激励其选择高投资额Ph, 需要保证(4.22) 式成立。 如果B1 的估值是L, 项目发起方为了使其选择投资Pl 而不是放弃参与众筹项目, 需要保证(4.23) 式成立。
此外, 我们可以得到不同情形下项目发起方的期望收益, 从而构建出如下所示的优化问题:
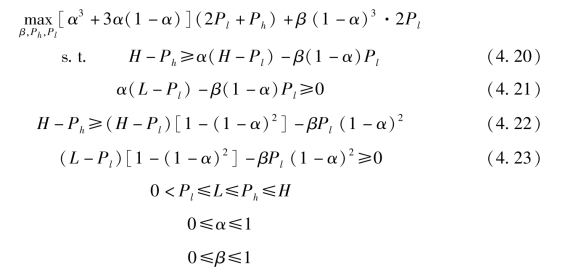
同样地, 由于上述模型难以直接求解, 我们通过一个数值算例来进行分析。假设H=50, L=10, 考虑潜在支持者具有高估值的概率α 从0 到1 变化, 我们可以得到如表4.7 和图4.5 所示的结果。
表4.7 菜单定价策略下高估值概率变化时的结果(T=2Pl +Ph)
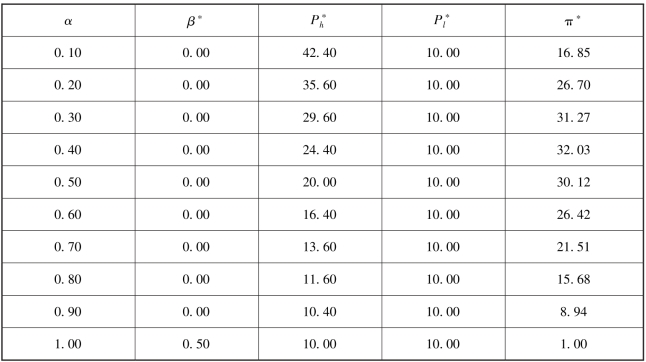
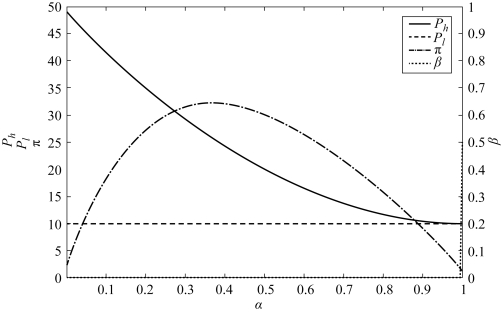
图4.5 菜单定价策略下不同高估值概率的结果(T=2Pl +Ph)
观察上述图表, 我们可以得到如下结论:
结论4.2 在三阶段模型中, 当菜单定价策略的众筹目标为T =2Pl +Ph 时,可以发现:
·β =0, 即AON 机制是项目发起方的最优选择。
·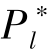 =L,
=L, 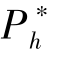 随着α 的增大单调递减; 当α=1 时,
随着α 的增大单调递减; 当α=1 时,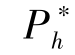 =L。
=L。
·π是关于α 的凹函数。
与两阶段模型中菜单定价策略下的结论类似, AON 机制是项目发起方的最优选择。 需要注意的是, 与(1) 相比, 此时筹资目标T =2Pl +Ph, 相对更小、更容易实现。 这意味着, 只要有一个具有高估值的潜在支持者到达, 众筹项目就能够获得成功。 因此, 与(1) 中α 较大的情形类似, 我们可以发现β =0 且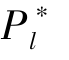 =L。
=L。
当α 很小时, 由于具有高估值的潜在支持者出现的可能性很低, 所以, 项目发起方应制定一个较高的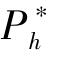 以获取尽可能高的期望收益。 随着α 不断增大, 为了激励具有高估值的潜在支持者选择高价格,
以获取尽可能高的期望收益。 随着α 不断增大, 为了激励具有高估值的潜在支持者选择高价格, 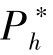 会不断下降。 最终, 当α =1时,
会不断下降。 最终, 当α =1时, 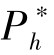 =L。 但与此同时, 也能够发现, 当α 较大时, 虽然众筹项目成功率增加, 但由于
=L。 但与此同时, 也能够发现, 当α 较大时, 虽然众筹项目成功率增加, 但由于 较低, 项目发起方的期望收益也会受到影响。
较低, 项目发起方的期望收益也会受到影响。
如果对比如表4.6 和表4.7 所示的结果, 我们可以发现, 若α≤0.4, 具有高估值的潜在支持者出现的可能性比较小。 此时, 项目发起方设置众筹目标为T =2Pl +Ph 可获得较高的收益, 而且其应该采用AON 机制。 当α >0.4 时, 具有高估值的潜在支持者出现的可能性增加, 那么, 众筹目标应设定为T =2Ph +Pl。而β随着α 的增大先增加到1 后变为0。 大约在α=0.7 时, 项目发起方可以取得最大的期望收益。
为了进一步验证上述结论, 我们对不同的H 和L 的组合进行了计算, 发现H/L 取值变化时, 项目发起方的最优决策也会相应发生变化。 我们发现, 当H/L <2 时, 发起方的众筹机制选择会发生变化。 例如, 取H =50 和L =30, 相应的结果如表4.8 和4.9 所示的结果。
表4.8 菜单型定价策略下高估值概率变化时的结果(T=2Ph +Pl)
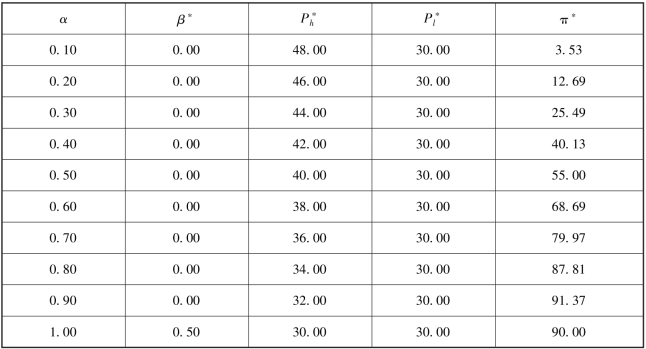
表4.9 菜单型定价策略下高估值概率变化时的结果(T=2Pl +Ph)

续表
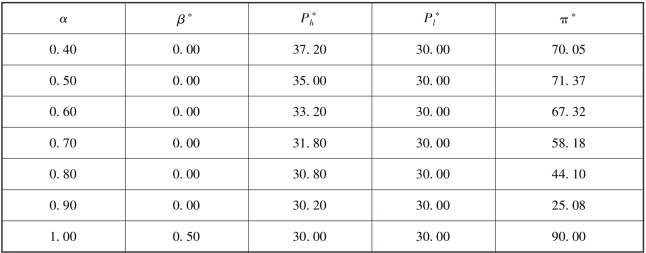
观察上述两个表格的结果, 我们可以发现, 无论众筹目标如何设计, 项目发起方都会选择AON 机制(即β =0。 应注意到, α=1 时, 项目必然成功, β =
0.5 无实际意义)。 这意味着, 当潜在支持者的估值差异较小时, 众筹项目成功的可能性相对增大。 因此, 对项目发起方来说, 应更多地考虑通过选择合理的机制促使项目成功(即采用AON 机制), 而不是考虑在项目失败时获得尽可能多的筹资金额。
总结菜单定价策略下我们所得到的结果, 可以发现, 只有当潜在支持者估值差异较大且具有高估值的支持者出现可能性较小时, 项目发起方才应该采用混合机制。 在其他的大多数情况下, AON 机制都是占优的。
4.3.1.6 四种定价策略的比较
上文中, 我们给出了四种不同定价策略下, 项目发起方的众筹机制选择以及相应的最优定价。 对于前三种定价策略, 我们能够给出项目发起方最优定价的显示解, 相关结果如表4.10 所示。
表4.10 离散型估值分布下三种定价策略结果比较

续表

结合表4.10, 一方面, 我们可以发现, 在这三种策略下, 项目发起方始终应选择AON 机制。 另一方面, 我们可以直接得到如下定理。
定理4.4 在三阶段模型下,
·当![]() 时, 项目发起方在数量型策略下的期望收益大于跨期定价策略; 反之, 当
时, 项目发起方在数量型策略下的期望收益大于跨期定价策略; 反之, 当![]() 时, 跨期型定价策略下的期望收益大于数量型策略。
时, 跨期型定价策略下的期望收益大于数量型策略。
·当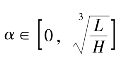 时, 项目发起方在数量型策略下的期望收益大于利润型策略; 反之, 当
时, 项目发起方在数量型策略下的期望收益大于利润型策略; 反之, 当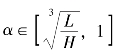 时, 利润型策略下的期望收益大于数量型策略。
时, 利润型策略下的期望收益大于数量型策略。
·当![]() 时, 项目发起方在跨期定价策略下的期望收益大于利润型策略; 反之, 当
时, 项目发起方在跨期定价策略下的期望收益大于利润型策略; 反之, 当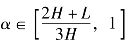 时, 利润型策略下的期望收益大于跨期定价策略。
时, 利润型策略下的期望收益大于跨期定价策略。
但是, 在菜单定价策略下, 我们未能给出项目发起方最优定价及最大期望收益的显示解。 因此, 我们采用与前面算例相同的参数(H=50 和L =10) 计算其他三种定价策略下发起方的期望收益, 可以得到如图4.6 所示的期望收益。
我们可以发现, 当潜在支持者具有高估值的可能性较小时, 对项目发起方来说, 数量型策略具有较大优势, 因为使用低价可以保证潜在支持者都会参与众筹项目。 当潜在支持者具有高估值的可能性居于中等水平偏下时, 菜单定价策略更有优势。 这是因为, 该策略在提高出价的基础上尽可能激励潜在支持者参与众筹项目, 同时还通过采用混合机制, 保证在项目失败时, 项目发起方仍然能够获得一定的收益。 而当潜在支持者具有高估值的可能性处于中等偏上水平时, 跨期定价策略逐渐显现出优势。 因为跨期定价策略的定价整体高于菜单定价策略, 且此时潜在支持者具有高估值的可能性不断提升, 所以, 跨期定价策略能够为发起方带来更高的期望收益。 当潜在支持者具有高估值的可能性足够大时, 利润型策略具有明显的优势。
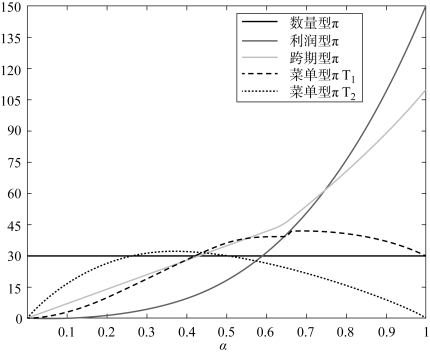
图4.6 离散型估值分布下四种定价策略项目发起方的期望收益
相比于两阶段情况下项目发起方在离散型估值分布下的策略, 我们发现, 三阶段模型的结论有很多相似之处。 总体来看, AON 机制在大多数情况下对项目发起方来说都是最优的选择, 而具体定价策略的选择则要依据潜在支持者的估值分布来确定。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






