4.2.2.1 模型描述

在支持者估值服从连续分布的假设下， 若支持者B1 和B2 的估值分别为V1和V2， 且满足独立同分布的基本条件。 那么， 此时众筹成功的条件应是B1 和B2的估值都不小于两个阶段项目发起方的定价P1 和P2， 其概率是Prob｛V1≥P1 and V2≥P2｝， 此时， 发起方可以获得全部的众筹金额。 若众筹失败但B1 进行了投资， 则发起方仍可以获得筹资金额βP1， 其概率是Prob｛V1≥P1 and V2 ＜P2｝。 需要注意， 此情况发生的条件是B1 选择投资的期望效用不小于0。

根据上述分析， 项目发起方的期望收益可表示为

化简（4.8）， 可以得到

将该结果带入（4.7）， 可以将目标函数转化为:

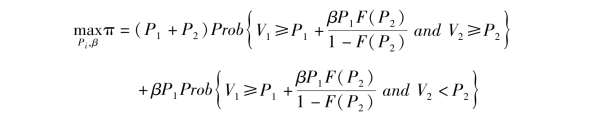
最终， 项目发起方为了最大化其期望收益， 需要解决以下优化问题:

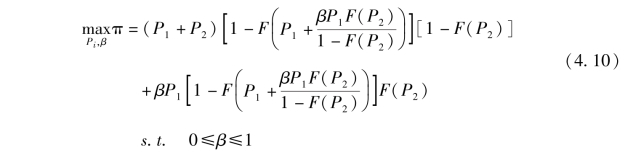
由于以上优化问题较为复杂， 难以直接求解分析。 为了得出具有可操作性的结论， 我们在后文中只考虑两种较为简单的情形， 即支持者估值分布服从均匀分布和正态分布两种常见分布的情况。

4.2.2.2 支持者估值服从均匀分布的情形

在均匀分布下， 我们假设两个潜在支持者的估值Vi（i =1， 2） 服从［0， N］的均匀分布（N ＞0）。 那么， Vi 的密度分布函数为f（Vi） =1/N， 累积分布函数为F（Vi） =Vi/N。 由于Vi∈［0， N］， 所以， 应有Pi∈［0， N］， 以保证众筹定价在支持者估值的区间内浮动。

将累积分布函数带入（4.10） 式， 可以得到如下的优化问题:

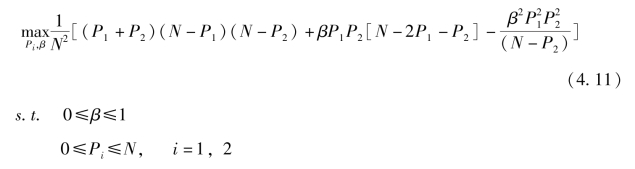
求解上述优化问题， 可以得到如下定理。

定理4.2 当支持者估值服从均匀分布时， 项目发起方的最优定价P*1 可以在［2N/9， N/3］ 上任意取值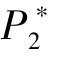， =N/3， 相应的β* =2N/3P 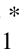-2。 此时， 项目发起方的最大期望收益为π* =8N/27。

证明： 根据（4.11） 的优化问题， 容易求得:

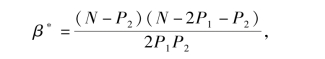
进而发起方的期望收益可以写成:

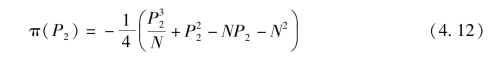
对P2 求一阶导数， 结果为:

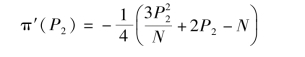
对P2 求二阶导数， 结果为:(www.daowen.com)

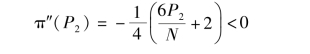
所以， π（P2） 是P2 的凸函数。 令一阶导数等于0， 容易解得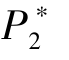=N/3。 进而可以得到:

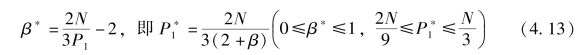
将上述最优解代入目标函数中， 容易得到π* =8N/27。

证毕。

上述定理给出了当支持者的估值满足均匀分布时， 项目发起方的最优决策。该决策具有如下特点。

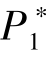· 小于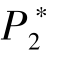。 这意味着第一阶段的定价低于第二阶段， 能够更好地吸引潜在支持者参与到众筹项目中。

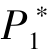· 和β*可以在一定范围内自由变化。 注意到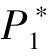， 越大， β*的取值越小。 这意味着， P1* 的值会影响到项目发起方所选择的众筹机制。 特别地， 当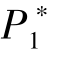=N/3 时， β* =0， 此时两个阶段的定价完全相同， 发起方采用AON 机制；而P1* =2N/9 时， β* =1， 发起方应采用KIA 机制。

为了进一步验证上述结论， 我们设计了如下的数值算例: 取N 从1 到500，使用Matlab 工具求解优化问题（4.11） 的最优解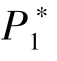、 、 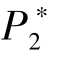β*， 以及取得最优解时的最大收益π*， 可以得到如图4.1 所示的估值服从均匀分布的最优定价与期望收益。

在该算例中， 我们选择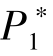 =5N/18。 注意: 的可行范围是［2N/9， N/3］。 从图4.1 中可以看出， 此时， 混合机制是项目发起方的最优选择， 即β*的取值大于0 小于1 （而且与N 无关）。 同时， 的值始终大于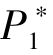 ， 这也验证了上述的结论。

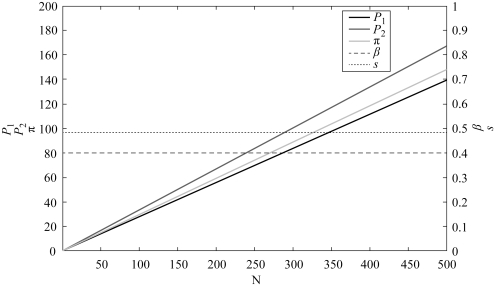
图4.1　估值服从均匀分布的最优定价与期望收益

4.2.2.3 支持者估值服从正态分布的情形

这里， 我们假设支持者的估值Vi 服从N（μ， σ2） 的正态分布。

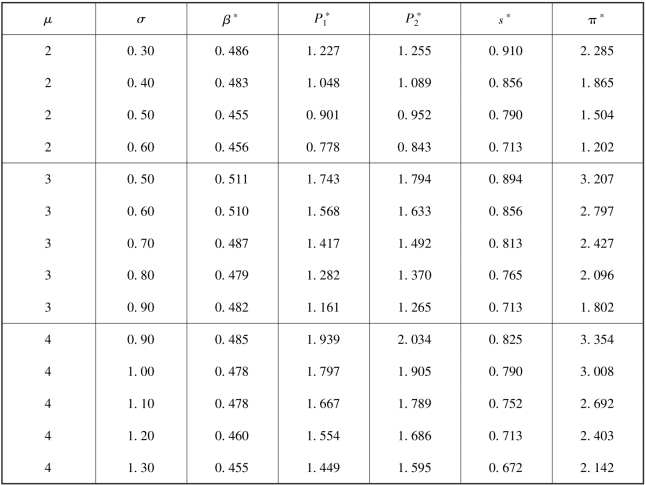
由于难以直接对模型进行求解， 所以， 我们通过数值算例的方式， 对项目发起方的最优决策以及相关的期望收益进行分析。 表4.3 展示了数值算例的结果。我们将算例划分为四组， 每一组中支持者估值的均值μ 固定， 通过变化标准差σ来分析发起方的最优决策。 需要注意的是， 支持者的估值Vi 通常应不小于0， 所以我们假设μ ＞3σ。

观察表4.3 的结果， 我们可以得出如下结论。

①在μ 恒定的前提下， 当σ 增大， 即支持者的估值分布更加分散时， 若仍保持原来的定价， 估值高于该定价的支持者存在的可能性会下降， 这将降低项目的成功率。 所以， 为了维持较高的项目成功率， 项目发起方需要降低两阶段的定价， 获得的收益也随之下降。

②最优定价决策满足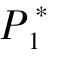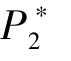＜＜μ。 为了提高项目筹资的成功率， 两阶段的最优定价都低于估值分布的均值。 同时， 由于β*的存在， B1 投资的风险相对较大， 且B1 的投资对B2 的参与有正向激励作用。 所以， 为了在第一阶段鼓励潜在支持者参与众筹项目， 发起方设定的第一阶段定价应低于第二阶段。

③β*的取值具有双重意义。 如果β*太高， 会使得B1 承担的风险过高， 阻止其参与众筹； 如果β*太低， 又会使得发起方在项目失败时得到的收益减少。 根据数值算例的结果， 我们发现的β*取值范围主要集中在［0.4， 0.5］， 处在中间水平以下的位置。 这说明了降低B1 承担的风险更为重要， 整体来说更有利于提高项目发起方可获得的收益。

表4.3　支持者估值服从正态分布时发起方的最优决策

续表