4.2.1.1 模型描述

不考虑发起方采用哪种具体定价策略， 假设其在众筹两个阶段分别定价为P1 和P2， 并设定一个规定期限内的筹资金额目标， 用T 来表示。 注意， 应有T=P1 +P2。

我们假设众筹项目的潜在支持者都是理性的。 对于一个两阶段的问题来说，第二个阶段到达的潜在支持者B2 （其估值为V2） 的决策比较简单， 只要投资金额小于等于其估值， 则B2 必然会参与到众筹项目中。 对于第一个阶段到达的潜在支持者B1 （其估值为V1）， 则需要考察其期望效用是否不小于0。 很显然， 对B1 来说， 当其在第一阶段进行投资后， 若众筹成功， 则其效用为V1 -P1； 若众筹失败， 则其效用为-βP1 （即发起方保留的筹资金额）。

假设众筹成功的概率为s。 那么， 该概率与众筹项目在两个阶段的定价以及支持者的估值有关。 因此， B1 参与众筹项目的条件为:

而对发起方来说， 如果在两个阶段当中投资金额达到筹资目标， 则发起方获得P1 +P2。 否则， 若项目失败， 存在两种情形:

（i） 第一个阶段到达的支持者进行了投资， 但第二个阶段到达的支持者发现项目无法成功， 则不会参与到众筹项目中， 此时， 发起方能够保留的金额为βP1。

（ii） 第一个阶段到达的支持者未进行投资， 则第二个阶段到达的支持者也不会参与其中， 此时， 发起方的收益为0。

因此， 在不考虑众筹运营成本等其他各类成本的前提下， 项目发起方的期望收益为:

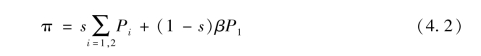
4.2.1.2 四种定价策略的分析与求解

在这一部分当中， 我们将分别讨论在四种不同定价策略下， 项目发起方应选择的众筹机制以及相应的最优定价决策。

（1） 数量型策略

很显然， 项目发起方在两阶段的定价为Pi =L（i=1， 2）， 并设定筹资目标为T=2L。 此时， 无论两个阶段到达的支持者的估值是H 还是L， 他们都愿意参与到众筹项目中， 其投资金额为L。 所以， 众筹项目一定能够成功， 也就是说众筹成功的概率s=1。

此时， β 的取值对众筹结果没有影响， 而项目发起方的期望收益为π* =2L。

（2） 利润型策略

在该策略下， 项目发起方在两阶段的定价为Pi =H（i =1， 2）， 并设定筹资目标为T=2H。 很显然， 只有当两阶段的支持者的估值都是H 时， 众筹才可能成功。

对B2 来说， 如果他的估值是H， 且B1 已投资， 那么， B2 一定会投资； 否则， B2 不会投资， 众筹项目失败。 而对B1 来说， 如果他的估值是H， 则众筹成功的概率为α （B2 的估值为H）。 此时， B1 的期望效用为E1 =α（H -H） -（1 -α）βH≤0。 显然， 只有当β=0 时， E1 =0， B1 才会投资。

所以， β* =0， 即发起方应选择AON 机制。 此时， 众筹项目成功的概率为s=α2， 项目发起方的期望收益为π* =2α2H。

（3） 跨期定价策略

与Hu 等（2015） 类似， 在跨期定价策略下， 我们假设项目发起方在两阶段的定价是（H， L） 或（L， H）， 并设定筹资目标为T=H+L。

显然， 当发起方的定价为（H， L） 时， 只需要讨论B1 的估值是H 时的情形。 与利润型策略类似， 容易得到β* =0， 即发起方应选择AON 机制。 此时，项目成功的概率是α， 而发起方的期望收益为π* =α（H+L）。

而当项目发起方的定价为（L， H） 时， 需要分两种情况进行讨论。

①B1 的估值是L 时:

若β=0， 则B2 的估值是H 时项目成功， B1 的效用是0； 而B2 的估值是L 时项目失败， B1 的投资被全部退回， 所得效用仍然是0。 所以， 该情况下B1 会参与到众筹项目中。 此时， 项目成功的概率为s =（1 -α）α， 发起方的收益为π =（1 -α）α（H+L）。

若β ＞0， 当B2 的估值是H 时， B1 的效用为0； 当B2 的估值是L 时， 若B1参与众筹， 则其效用为-βL， 所以， B1 的期望效用为E1 = -（1 -α）βL ＜0。 因此， 该情况下B1 不会参与众筹， 项目必然失败。

综上可知， 当B1 的估值是L 时， β* =0， 即发起方应选择AON 机制。

②B1 的估值是H 时:

与情况①的分析过程类似， 在β=0 的情况下， B1 的期望效用E1 =α（H-L） ＞0， 故B1 愿意参加众筹。 此时， 项目成功的概率为s=α2， 发起方的期望收益为π=α2（H+L）。

若β ＞0， 则B1 的期望效用为E1 =α（H -L） -（1 -α）βL。 令E1 ≥0， 可以得到:(www.daowen.com)

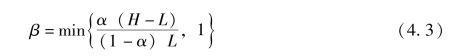
此时， 项目发起方的期望收益为:

很显然， β 越大， 发起方的期望收益越高。 因此， 根据（4.3） 式， 可以得到: 当αH ＞L 时， β* =1， 此时π =α（αH +L）； 当αH≤L 时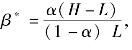， 此时π=2α2H。

综合上面的分析， 在跨期定价策略的两种定价方式下， 最优的运作机制以及发起方的期望收益如表4.1 所示。 我们可以进一步比较两种定价方式下发起方的期望收益， 选出其中一种更具优势的定价方式。 显然， α（H +L） ＞α（αH +L），并且， 当αH≤L 时， 可以得到α（H+L）≥2α2H。 由此可得， 采用（H， L） 的定价方式可以获得较高的期望收益。 所以， 项目发起方选择跨期定价策略时， 应设置价格为（H， L）， 但对运作机制并没有严格的要求， 无论β 取何值， 都不会影响最终发起方的期望收益。 同时， 通过上述分析也可以发现运作机制与支持者决策之间的关系: 若第一阶段的定价对于B1 来说没有任何剩余价值， 那么发起方只能选择AON 机制； 若B1 的估值高于定价， 那么他愿意承担一定风险选择投资， 此时发起方可以设置非AON 的运作机制。

表4.1　两阶段跨期定价策略的结果

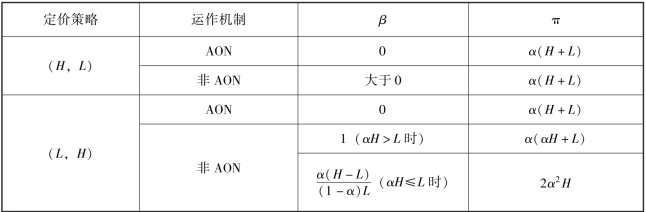
（4） 菜单定价策略

与Hu 等（2015） 类似， 我们假设项目发起方在两阶段的菜单定价为（Ph，Pl）， 且菜单定价满足条件Pl≤L≤Ph≤H。 此时， 众筹项目的筹资目标为T=Ph +Pl。 对每个潜在支持者来说， 每个阶段均可选择投资Ph 或Pl。 显然， B2 的决策与B1 的决策密切相关， 而B1 则要考虑B2 的估值做出自己的决策。

当两个支持者的估值都是L 时， 项目一定会失败， 发生这种情况的概率是（1 -α）2。 除此之外， 项目理论上应该能够成功， 所以， 项目成功的概率为s =1 -（1-α）2 =α（2-α）。

对项目发起方来说， 众筹项目的设计可以用以下机制设计问题来描述:

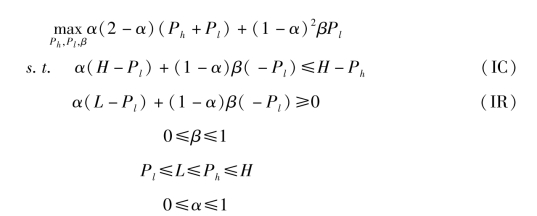
其中， （IC） 是激励相容条件， 含义为: 当B1 的估值是H 时， 投资Ph 的期望收益要高于选择Pl， 从而促使B1 选择高价。 （IR） 为理性约束条件， 即当B1的估值是L 时， 选取低价Pl 投资时期望效用也不小于0。 另外， 目标函数中的第一项描述了众筹成功时发起方的期望收益， 而第二项则描述了众筹失败时发起方的期望收益。

定理4.1 在两阶段的菜单定价策略下， 项目发起方的最优定价为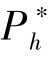 =（1 -α）H+αL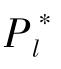， =L 且β* =0。 这意味着发起方应采用AON 机制， 此时其最优的期望收益为π* =α（1 -α）（2 -α）H+α（2 -α）（1 +α）L。

证明： 对于项目发起方来说， Ph 和Pl 的定价应尽可能高， 以获取更高的收益。 根据前述（IR） 条件以及Pl 的取值范围可得:

将（4.5） 式带入（IC） 条件， 考虑Ph 的取值范围， 可以得到:

将（4.5） 和（4.6） 带入目标函数， 则发起方的期望收益如下:

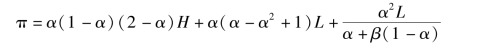
显然， β 越小， 发起方的期望收益越大。 故而得到， β* =0 且P*

l =L， 发起方的最大期望收益为π* =α（1 -α）（2 -α）H+α（2 -α）（1 +α）L。

证毕。

所以， 若项目发起方选择菜单定价策略， 应选择AON 机制， 并按照上述定理给出最优的菜单定价， 以获得最大的期望收益。

4.2.1.3 四种定价策略的结果比较

在离散型的支持者估值下， 对比项目发起方分别采用四种定价策略时获得的期望收益， 可以得到如表4.2 所示的两阶段离散型估值分布的四种定价策略比较的结果。

表4.2　两阶段离散型估值分布的四种定价策略比较的结果

通过表4.2， 可以发现在支持者估值为两点分布时， AON 机制是广泛有效的。 所以， 项目发起方对不同定价策略的选择条件， 仍然可以参考Hu 等（2015） 中的命题1。

然而， 支持者的估值服从两点分布， 只是一种非常特殊的情况， 适用于部分产品。 在另外一些场景下， 我们通常假设支持者的估值服从一般的连续分布。 那么， 在这种情况下， AON 机制是否仍然最优， 值得进一步讨论。 这也是我们在下一个小节中将要回答的问题。