在稳健性检验部分， 我们选取筹资进度这一变量作为研究的因变量， 考虑回报菜单中的四类变量， 在衡量众筹成功的指标发生变化时， 影响效力是否发生改变。 上文中的其他自变量也将作为控制变量带入方程。 筹资进度为连续型数值变量， 使用多元线性回归模型更符合研究需求。

线性回归模型应满足正态性、 等方差、 零均值、 无自相关性、 相互独立性的假设， 对变量的分布要求较高。 因此， 在稳健性检验部分， 我们在上文单位变化的基础上， 对部分偏态分布的、 均值远小于标准误差的控制变量做了取对数处理。 具体来看， 取对数的变量包括筹资目标、 关注人数、 点赞人数三项。 下文使用变换后的变量进行统计分析， 描述性统计与相关性分析结果与3.2.3 节一致。依据回报菜单中的变量将多元线性模型扩展为四个分析维度， 回归结果如表3.6所示。 表中第一列检验了除回报菜单因素外， 其余变量对模型的总体贡献； 第二列检验了回报菜单中， 最小、 次小两项价格因素对筹资进度的影响； 第三列检验了回报档数与优惠档数两项档数因素对筹资进度的影响； 第四列将所有自变量带入方程， 与前三列回归结果形成对比。

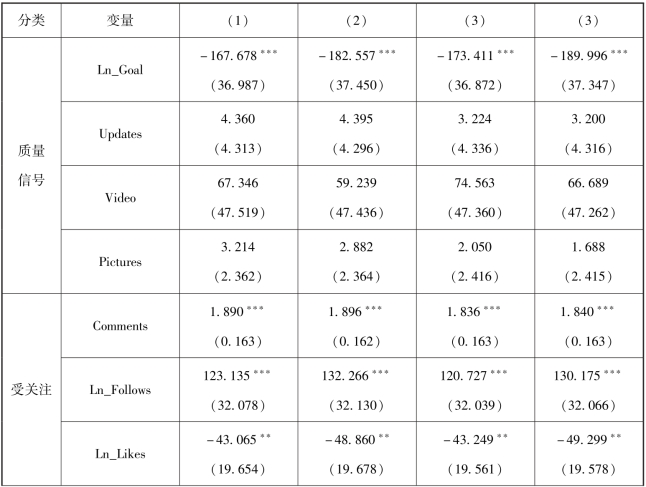
表3.6　多元线性回归结果

续表(www.daowen.com)

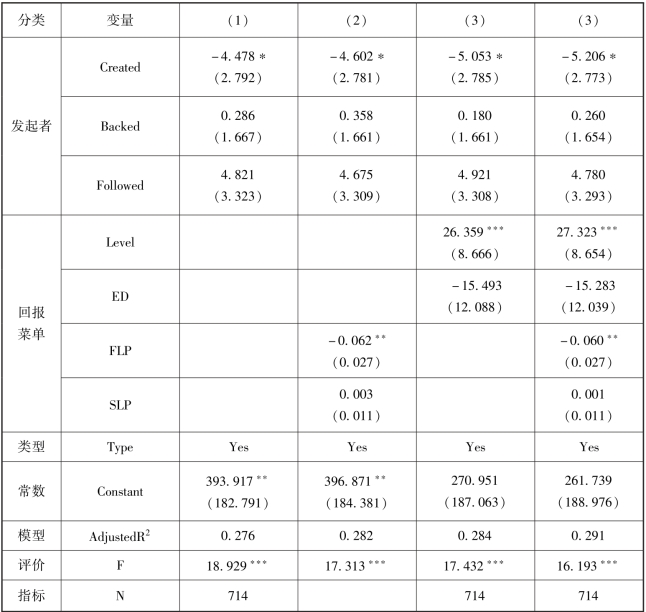
注: 括号内数值为标准误；***、**、 *表示估计系数达到1%、 5%、 10%的显著性水平。

回归结果中关键自变量的显著性水平与影响方向与上文相似。 评价模型效果的指标中， Adjusted R2值均高于0.27， 模型具有一定的解释效力。 增加研究的自变量时， Adjusted R2值同样增加， 证实了我们所关注的变量确实会对项目的筹资进度产生影响。 此外， F 检验结果显著， 自变量之间不存在共线性问题， 控制变量的相关方向和显著性在四个分析维度中基本保持稳定， 模型的适用性良好。

多元线性回归结果中的第一列首先检验了控制变量对筹资进度的影响。 与3.2.4 节的研究结论一致的是， 话题数量、 关注人数对筹资进度有显著正向影响； 筹资目标、 点赞人数和发起方的已发起经历对筹资进度有显著负向影响。 此外， 当筹资进度成为衡量众筹成果的指标时， 进展更新、 视频数量、 图片数量和发起方已关注经历不再对其产生显著影响。 回归结果中的第二列检验了回报菜单中最小和次小筹资金额对筹资进度的影响。 稳健性检验结果表明， 最小筹资金额设置越大， 对筹资进度越不利， 这一变量的显著性程度与上文相比有所上升（β= -0.062， Sig.=0.023）。 次小筹资金额对筹资进度产生正向影响， 但显著性水平未达到10%的标准（β=2.278， Sig.=0.771）。 回归结果中的第三列检验了回报档数和优惠档数对筹资进度的影响。 结果显示， 在保持其他因素不变的情况下， 回报档数越多， 筹资进度越高（β =26.359， Sig.=002）， 项目取得成功的可能性因此提高。 当在模型中加入最小和次小档筹资金额时， 这一结论保持不变。 与成败场景下的研究结果相似， 优惠档数与筹资进度之间呈现负相关关系，但负向关系不显著（β= -15.493， Sig.=0.200）。 出现这一结果的原因可能是，优惠档位对潜在支持者投资决策的影响不仅仅与优惠档位的数量有关， 还可能取决于优惠的力度或享受优惠的门槛等因素。