由交流电源、负载、连接导线、开关等组成的电路称为交流电路。交流负载有纯电阻、纯电感、纯电容或其组合。电源中只有一个交流电动势的交流电路称为单相交流电路。

(一)电阻交流电路

实际应用的白炽灯、电烙铁、电阻器等可看成电阻元件。在电阻元件构成的交流电路中,电流和电压的频率相同,相位相同,完全符合欧姆定律,即

电阻电路的相量图和波形图,如图1-27所示。

任何瞬间电阻上所消耗的功率等于通过电阻的电流与加在电阻两端电压的瞬时值的乘积,即

从图1-27(c)可以看出,任一瞬间的功率数值都是正值,说明电阻电路中总是从电源吸取能量,也就是说电阻是一种耗能元件。

电阻元件的平均功率等于流过电阻的电流、两端施加的电压的有效值的乘积,即

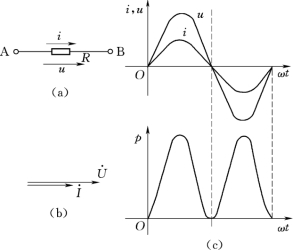
图1-27　电阻电路的相量图和波形图

(a)电阻电路图;(b)相量图;(c)u、i、p波形图

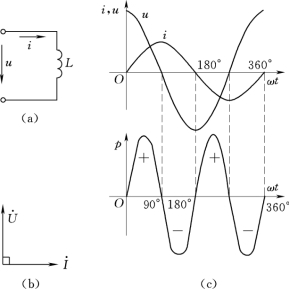
图1-28　电感电路的相量图、波形图

(a)电感电路图;(b)相量图;(c)u、i、p波形图

(二)电感交流电路

实际应用中的荧光灯镇流器线圈、接触器的线圈、继电器的线圈、电动机的绕组等,若忽略它们的导线电阻,都可看成是电感元件。图1-28所示为纯电感电路及其相量图、波形图。

在电感交流电路中,电压和电流的有效值或最大值之比称为电感电抗,简称感抗,用XL表示,即

感抗XL和电阻R相似,在交流电路中都起阻碍电流通过的作用。XL的大小与电感L和频率f的乘积成正比,即

式中 L——绕组(线圈)的电感,H;

f——电源电压的频率,Hz;

ω——电源电压的角频率,rad/s;

XL——感抗,Ω。

从图1-28(c)中看出,电压和电流的频率相同,电压的相位超前于电流90°,用瞬时值表示为

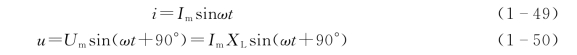
从图1-28(c)中的功率波形图看出,瞬时功率是一个两倍于电压(或电流)频率的正弦曲线,且曲线的正、负半周完全对称。正值表示从电源吸取能量,负值表示向电源放出能量,从而得知电感元件从电源吸取的平均功率为零,即电感没有消耗能量,只是在电源和电感线圈之间有周期性的能量互换。因此,电感是一种储能元件。在电源和电感线圈之间互相转换功率的规模(瞬时功率的最大值)称为感性无功功率,用QL表示。

【例1-7】 有一线圈,电感L为10mH,电阻可忽略不计,将它接在电压u=311sinωt(V),频率为50Hz的电源上。试求线圈的感抗、电路中通过的电流、电路中的无功功率,并写出电流瞬时值的表达式。

解:线圈的感抗:XL=2πfL=2×3.14×50×0.01=3.14(Ω)(www.daowen.com)

通过线圈的电流: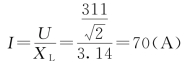

无功功率:

电流瞬时值的表达式:i=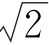×70sin(ωt-90°)=99sin(ωt-90°)

(三)电容交流电路

任何两块靠近的金属导体(又称极板),中间用不导电的绝缘介质隔开,就形成了电容器。把电容器接在电源上,电容器中就储存了电荷。其两个极板总是分别带有电量相等的正、负电荷。表示电容器储存电荷电量能力的物理量,称为电容器的电容量(简称电容),用符号C表示。C值愈大,表明电容器所储存的电量愈多。用公式表示为

式中 Q——极板上的带电量,C;

U——两个极板之间的电压,V;

C——电容,F(法拉)。

法拉(F)这个单位太大了,一般用微法(μF)或皮法(pF)做电容的单位。

1μF=10-6F;1pF=10-6μF=10-12F

电容交流电路中电压和电流的有效值(或最大值)之比等于电容电抗,简称容抗,用XC表示。

容抗在电路中也起阻碍电流的作用。XC的大小与电容C和频率f的乘积成反比,即

式中 C——电容元件的电容,F;

f——电源交流电压的频率,Hz;

ω——电源交流电压的角频率,rad/s;

XC——容抗,Ω。

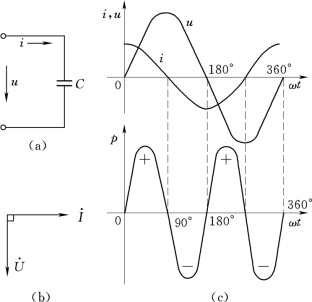
图1-29　电容电路的相量图和波形图

(a)电容电路图;(b)相量图;(c)u、i、p波形图

电容元件中的电流与电压的频率相同,但电流的相位超前于电压90°,如图1-29所示。电容电路中电压电流的瞬时值为

从图1-29(c)看出,在电容电路中,其瞬时功率的频率也是两倍于电压(或电流)的频率,在一个周期内的平均值也等于零。说明电容电路中也不消耗能量,在电源和电容器间只有周期性的能量交换。它也是一个储能元件。这种互相转换功率的规模(最大值)称为电容性无功功率,用QC表示

QC的单位也是var。

【例1-8】　一只1μF的电容器两端加上正弦电压u=220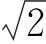sin(314t-30°)(V),求通过电容器中电流的有效值,并写出电流的瞬时值表达式。

解:电容器的容抗:

通过电容器电流的有效值:

电流的初相位φ=90°-30°=60°,则电流的瞬时值表达式为