正弦交流电一般有三种表示方法:解析法、曲线法、相量图法。一个正弦量的相量图、波形图、解析式是正弦量的几种不同表示方法,它们是一一对应的关系。

(一)解析法

利用正弦函数表达式形式表示正弦交流电的方法,也可称为瞬时值表示法。

(二)曲线法

在平面直角坐标系中作出曲线的方法称为曲线法,也称波形图法。横坐标表示电角度,或者时间,纵坐标表示电压(或电流,或电动势)大小。

作波形图一般采用五点作图法,如图1-24为函数u=100sin(100πt-π/6)的波形图。

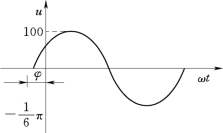
图1-24　函数波形图

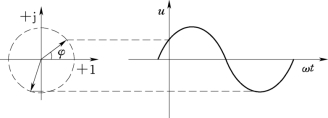
图1-25　振幅相量表示法(www.daowen.com)

(三)相量图法

如果要对正弦交流电进行加、减运算,无论是运用波形图还是解析式表达式,都不是很方便。为此,引入正弦交流电的相量图表示法。

用一个在直角坐标中绕圆点作逆时钟方向不断旋转的矢量来表示正弦交流电的方法称为旋转矢量法,也称为相量图法。正弦量可以用振幅相量或有效值相量表示。振幅相量表示法:用正弦量的振幅值作为相量的模(大小),用初相角作为相量的幅角,如图1-25所示。

图1-26　有效值相量表示法

有效值相量表示法:用正弦量的有效值做为相量的模(长度大小),仍用初相角做为相量的幅角。例如,函数u=50sin(100πt+45°)的有效值相量表示法如图1-26所示。

应用相量图时注意以下几点。

(1)同一相量图中,各正弦交流电的频率应相同。

(2)同一相量图中,相同单位的相量应按相同比例画出。

一般取直角坐标轴的水平正方向为参考方向,逆时针转动的角度为正,反之为负。有时为了方便起见,也可在几个相量中任选其一作为参考相量,并省略直角坐标轴。

正弦交流电用相量表示后,它们的加、减运算可按平行四边形法则进行。