乐清市1980～2000年21年的人口资料，如表1所示。

表1　　乐清市1980～2000年实际人口数　　单位：万人

2.1 一般预测方法

2.1.1 一元线性回归法

取1980～2000年21年的人口资料进行回归分析的回归模型如下

式中 y——各水平年人口规模；

x——年份，以公元纪年表示。

预测结果，如表2所示。

2.1.2 自然回归法

取1980～2000年21年的人口资料，按最小二乘法计算得回归方程为

式中 Xt——第t年人口数，万人；——第t+T年人口数，万人；

T——自回归滞后时段长，年。

据此预测不同水平年人口规模，如表2所示。

2.1.3 指数函数法

同样取1980～2000年21年的人口资料，建立指数函数方程，得

ln Y=0.015X-24.96

式中 X——预测人口水平年份；

Y——预测水平年人口数，万人。

据此预测不同水平年人口规模，如表2所示。

2.1.4 幂函数法

同样取1980～2000年21年的人口资料，建立幂函数方程，得

ln Y=15.08ln X-109.94

式中 X——预测人口水平年份；

Y——预测水平年人口数，万人。

据此预测不同水平年人口规模，如表2所示。

2.2 灰色模型

将灰色数列模型用于人口模型。现用该模型对乐清市人口进行分析预测。

（1）取1990年、1992年、1994年、1996年和1998年5年数据为原始数据列出表2。

表2　　乐清市的灰色人口模型数据表

（2）对原始数据列作一次累加生成(www.daowen.com)

x(1)(1)=x(0)(1)=1.027

x(1)(2)=x(0)(1)+x(0)(2)=2.076

︙

x(1)(6)=x(0)(1)+x(0)(2)+…+x(0)(6)=6.537

（3）构造累加矩阵B及常数项向量YN，得

（4）用最小二乘法求解灰参数a⌒，得

（5）代入微分方程模型，得

微分方程的时间函数解为

式中 x（1）（0）=x（0）（1）=1.027，代入

便得到GM（1，1）基本预测模型。

计算结果，如表2所示。

2.3 Logistic模型预测

2.3.1 Logistic生物模型讨论

由微分方程知识可知，对于p′=p（a-bp），0与a/b是它的临界点。

当P=0令p（t）=0+（ε）（t），∣ε（t）∣ ≤1，代入得ε′（t）=aε（t）

故知0点是不稳定的结点。

当p（t）=a/b，令p（t）=a/b+ε（t），∣ε（t）∣ ≤1，代入ε（t）=-aε（t）

故知a/b是稳定结点。

这表示种群将趋于稳定，当0＜p（t）＜a/b呈增长趋势，当a/b＜p（t）呈减少趋势，在a/b达到平衡。

对于

用分离变量法解得

即当种群未达到极限值a/b的一半时属加速增长，超过一半时属减速增长，但增长率仍为正的，随时间增加而减少，t→∞，p′→0。

2.3.2 乐清市城市人口的Logistic模型预测

选择1980，1990，2000间距相等的3个年份P（1980）=85.74、P（1990）=102.72、P（2000）=115.49，计算得a=0.05822，b=0.00042。

令，由于，得。代入得

将有关数据代入求得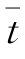=1971，a/b=137.07

计算各水平年的人口规模，如表2所示。

2.4 Leslie人口预测模型

利用第5次人口普查资料将乐清市人口按5年一个年龄段进行离散，得k-1时刻各年龄段人口数矩阵为P k-1和人口增长矩阵L如下所示，利用Leslie模型进行人口预测，结果如表3所示。