1.1 一般预测方法

1.1.1 一元线性回归法

该方法假定人口发展过程线上任一点的切线斜率基本保持不变，即各时期人口发展速度较一致，利用历史资料建立一元线性回归模型进行人口预测。将时间参数作为控制变量x，人口数量作为状态变量y，确定它们之间的数学模型y=a+bx。利用历史数据资料采用最小二乘法进行回归计算，计算回归系数 （公式如下），再根据水平年的时间来预测人口规模。

式中 xi——自变量，i=1，…，n，n为统计样本数；

yi——因变量，i=1，…，n；

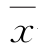——自变量均值；

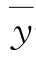——因变量均值。

1.1.2 自然回归法

人口数量在时间上的变化具有当前变化受前期数量影响的特殊性质，因此可以用自回归模型来预测其后期的数量。同样，利用历史数据资料采用最小二乘法进行回归计算，计算回归系数a、b，再根据水平年的时间来预测人口规模。

1.1.3 指数函数法

人口发展过程线并不都是近似于直线状，有些地区的人口前一段时期内发展较慢，越往后发展速度越快。例如，很多中小城市在城市化进程中人口发展过程就属于此类，这种情况下应选用指数函数模型。

式中，各符号的物理意义同式 （1）、式 （2）。

1.1.4 幂函数法

有些地区人口发展过程线前段时期发展速度较快，其曲线的斜率较大，越往后发展速度放慢，曲线的斜率逐渐减小，此时选用幂函数模型较为合适。

式中，各符号的物理意义同式 （1）、式 （2）。

1.2 灰色系统GM（1，1）法

总体来说，一个国家或相对较大区域的人口发展具有较明显的规律性，但对于较小区域来说人口发展规律并不一定呈线性或非线性函数关系，此类无规律可循或资料不全的情况下可以用灰色系统GM（1，1）来进行人口规模预测。步骤如下

第一步：选择任一子数列，并记作

第二步：对子数列作一次累加生成，得

其中　(www.daowen.com)

第三步：构造累加矩阵B与常数项向量YN，得

第四步：用最小二乘法求解灰参数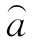，得

第五步：将灰参数代入时间函数，得

第六步：对x⌒（1）求导还原，得

第七步：计算x（0）（t）与x⌒（0）（t）之差及相对误差，得

第八步：利用上述模型进行预测。

1.3 Logistic人口预测模型

设p（t）表示在t时刻种群的大小，当种群很大时，可以认为p（t）是连续的，甚至可微的。如果b（t，p）表示t时刻单位时间种群里单个生物的出生率，d（t，p）表示t时刻单位时间种群里单个生物的死亡率，则r（t，p）=b（t，p）-d（t，p）表示t时刻单个个体的纯增率，于是

Δp=p(t+Δt)-p(t)≈r(t，p)p(t)Δt

令Δt0则有

当r（t，p）=a（常数）时，有 p′=ap，p（t0）=p 0

这就是Malthus人口律。

由于环境的限制，使得个体之间存在竞争结果使r（t，p）下降，于是荷兰生物学家提出添加竞争项——bp 2（b＞0），于是有

p′=ap-bp 2， p(t0)=p 0

这就是Logistic竞争的生物模型。

1.4 Leslie人口预测模型

该模型将整个人口按年龄段分为n个年龄段，在k-1时刻各年龄段人口数为P k-1，L为人口增长矩阵，有n+1行n列，对Leslie模型有P（k）=LP（k-1），据此可以进行人口预测。

式中 αi——各年龄段的生育率，i=1，…，n；

βi——各年龄段人口的存活率，i=1，…，n。