(1)如果 f(x)=A，且A ＞0 (或A ＜0)，则存在着点x0 的某一邻域，当x 在该邻域内(但x≠x0)时，f(x)＞0 (或f(x)＜0).

(2)如果f(x)≥0 (或f(x)≤0)，且f(x)=A，则A≥0 (或A≤0).

(3)如果在某一变化过程中，变量y 有极限，则变量y 一定是有界变量.

(4)f(x)=A f(x)=f(x)=A.

(5)变量y 以A 为极限的充分必要条件是变量y 可以表示为A 与无穷小量的和.

(6)有限多个无穷小量的代数和仍是无穷小量.

(7)有界变量与无穷小量的乘积是无穷小量.

(8)常量与无穷小量的乘积是无穷小量.

(9)任意多个无穷小量的积仍是无穷小量.

(10)若β 是无穷大量，则是无穷小量；

若α 是无穷小量，且α≠0，则是无穷大量.

(11)运算法则：

在某个变化过程中，如果limx，limy 都存在，则

当limy≠0 时，lim

(12)极限存在准则：(www.daowen.com)

准则1： 若在某个变化过程中，三个变量x、y、z 满足y≤x≤z，并且lim y =lim z =A，则limx=A.

准则2： 单调有界变量一定存在极限.

(13)两个重要极限：

①=1.

=1 的特征： 是“” 型.

容易推出： =1， =1.

②=e.

=e 的特征： 是“” 型.

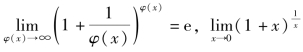容易推出：=e.

(14)闭区间上连续函数的性质：

有界性定理： 如果函数y =f(x)在闭区间[a，b] 上连续，则它在这个区间[a，b]上有界.

最值定理： 如果函数y=f(x)在闭区间[a，b] 上连续，则它在这个区间[a，b] 上一定存在最大值和最小值.

介值定理： 如果函数y=f(x)在闭区间[a，b] 上连续，m 和M分别为其在[a，b]上的最大值与最小值，则对于m 与M 之间的任一实数c，至少存在一点ξ∈(a，b)，使得f(ξ)=c.

根的存在定理： 如果函数y=f(x)在闭区间[a，b] 上连续，且f(a)f(b)＜0，则至少存在一点ξ∈(a，b)，使得f(ξ)=0.