1.简答题.

(1)单调增加函数是否一定无界? 为什么?

(2)是否任何函数在定义域内都存在反函数?

2.选择题.

(1)下列各对函数中，相同的是(　).

(A)f(x)=，g(x)=x　(B)f(x)=ln x2，g(x)=2ln x

(C)f(x)=cosx，g(t)=cost　(D)f(x)=，g(x)=x+1

(2)设函数f(x)的定义域为，则函数f(x)-f(-x)的图形关于(　)对称.

(A)y=x　(B)x 轴　(C)y 轴　(D)坐标原点

(3)设函数f(x)的定义域为，则函数G(x)=f(x)·f(- x)- cos x 是(　).

(A)单调减函数　(B)有界函数

(C)偶函数　(D)周期函数

(4)y= 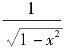-1 的定义域为(　).

(A)[-1，1]　(B)[-1，1)　(C)(-1，1)　(D)(0，1]

(5)设f(x)=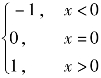，则f(-3)=(　).

(A)-1　(B)0　(C)1　(D)不存在

3.填空题.

(1)设f(x-1)=x2-2x，则f(x+1)=__________.(www.daowen.com)

(2)函数f(x)=的定义域是__________.

(3)设f(x)=，则f -1(x)=__________.

练习题参考答案

1.(1)不一定无界.例如，函数f(x)=1-在 内单调增加，但在(0， 内有界.

(2)不一定.例如，f(x)=x2 在定义域 的反函数不存在.

2.(1)(C).因为(C)中的函数定义域相等，且对应关系相同，所以选项(C)正确.而(A)，(B)，(D)三个选项中的每对函数的定义域都不同.

(2)(A).设F(x)=f(x)-f(-x)，则对任意x 有

F(-x)=f(-x)-f(x)=-F(x)

即F(x)是奇函数，因而，图形关于y=x 对称.

(3)(C).对任意x 有G(-x)=f(-x)·f(x)-cos(-x)=G(x)，即G(x)是偶函数，所以(C)正确.

(4)(C).因为要使函数y= 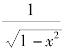-1 有意义，须1-x2≥0 且x2≠1，即x∈(-1，1).

(5)(A).因为x=-3 ＜0，所以f(-3)=-1.

3.(1)x2 +2x.设x-1 =t，则x=t+1，得f(t)=(t+1)2-2(t+1)=t2-1.

因此，f(x+1)=(x+1)2-1 =x2 +2x.

(2)(2，3)∪.ln(x-2)≠0，即x ＞2 且x≠3，得函数定义域为(2，3)∪(3，.

(3).