例1　求y= 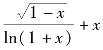的定义域.

[分析]　函数y = 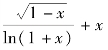中，同时包含平方根、分母、对数，所以，必须同时满足

1-x≥0，ln(1 +x)≠0，1 +x ＞0

解　要使函数有意义，必须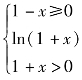≠0，即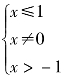，因而，所求函数的定义域是(-1，0)∪(0，1] .

例2　已知函数f(x+1)=x，求f(1)，f(ex).

[分析]　由f[g(x)] 先求出f(x)，可令t=x+1.

解　令x+1 =t，则x=t-1.

将x=t-1 代入f(x+1)=x 中，即有f(t)=t-1，所以

f(1)=1-1 =0

f(ex)=ex-1

例3　设=x，求

[分析]　f[f(x)] 中的“f(x)” 相当于f(x)中的“x”，在f[f(x)] 中，只要令t =f(x)即可.

解　令t=，得x=，将=x 转化成通常的显函数： f(t)=.

因而，=2.

例4　求函数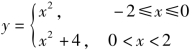的定义域.

[分析]　分段函数的定义域就是各段函数表达式取值范围的并集.

解　分段函数的定义域为[-2，0]∪(0，2)，即[-2，2).

例5　已知g(x)与f(x)=关于直线y=x 对称，求g(x).(www.daowen.com)

[分析]　关于y=x 对称的函数就是f(x)的反函数g(x)，所以g(x)=f -1(x).

解　由f(x)=，解得x=，因而，g(x)=.

例6　判断下列函数的奇偶性：

(1)f(x)=e -x2 +；(2)f(x)=ln(x+)；

(3)f(x)=x+cosx.

[分析]　在定义域内，偶函数满足： f(-x)=f(x)；奇函数满足： f(-x)=-f(x).

解(1)f(-x)=e -( -x)2 +=e -x2 +=f(x)，所以，f(x)=e -x2 +是偶函数.

(2)

因此，函数f(x)=ln(x+)是奇函数.

(3)f(-x)=-x+cos(-x)=-x+cos x，因而函数f(x)=x +cos x 既非奇函数又非偶函数.

例7　将下列函数分解成简单函数.

(1)y= ；(2)y=ln sin ；

(3)y=

[分析]　把复合函数分解成简单函数，首先要搞清楚它们的复合关系(结构)，然后再把它们拆成简单函数.

解(1)y= 可分解为y =eu，u =，v =sin x，即y = 由y =eu，u =，v =sin x 复合而成.

(2)y=ln sin可分解为y=ln u，u=sin v，v=，t=x3-1.

(3)y=可分解为y=，u=1 +2x +cosx.