时间—费用优化法可以解决的问题是：如何在费用增加最小的情况下缩短项目工期；或在保证期望的完工时间的条件下，所需要的费用最少；或在限制费用的条件下，项目的完工时间最短。

一般可以通过使用最小费用计划模型来实现时间—费用优化。该模型的基本假设是活动的完成时间与完成项目的费用之间存在一定的关系：一方面，要有资金来直接促进各项活动的进行；另一方面，需要资金来维持整个项目的进行。与促进单个活动有关的称为活动的直接费用，计入项目的总直接费用。这些费用可能是与人工有关的费用，如加班费、雇用更多工人的支出，以及从其他岗位调用工人的费用；而另一些可能与资源有关，如购买或租赁附加设备、高效率设备，以及借用辅助设施的支出。与维持项目的正常进行有关的费用称为项目的间接费用，包括日常管理费用、设施维修费用、资源的机会成本，以及在有合同约束下的罚款和奖金支出等。

活动的直接费用和项目的间接费用随时间的变化而出现不同方向的变化：一般情况下，时间缩短，直接费用上升，间接费用下降；时间延长，直接费用下降，但间接费用会上升。所以，编制时间计划的关键问题之一就是寻找具有最小总费用的项目工期，也就是时间和费用均衡的最优点。

我们曾在讨论项目生命周期时展示过如何压缩工期，下面我们再次讨论一下。找到时间和费用均衡的最优点的过程可分为5步。假设某项目有4项活动，间接费用在项目的前8天保持不变（10元/天），以后按每天5元的速度增加。

（1）绘制网络图，并标注必要信息，如图7-8所示。

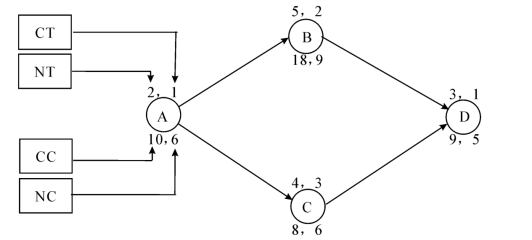
图7-8　时间-费用均衡示例（时间单位:天）

●正常时间（Normal Time），按照原先的时间进度计划，在正常条件下完成某项工作所需要的估计时间。

●正常成本（Normal Cost），在正常时间下完成某项工作所耗费的成本。

●赶工时间（Crash Time），在赶工的情况下完成某项工作的最快时间。

●赶工成本（Crash Cost），在赶工情况下完成某项工作所需要的成本。

这些信息也可以列在相关表格中，作为活动的细节说明。(www.daowen.com)

（2）确定每项活动的赶工费用率。赶工费用率可用公式（CC-NC）/（NTCT）直接计算得出，其过程如表7-2所示。

表7-2　计算得到每项活动的可赶工天数以及赶工费用率

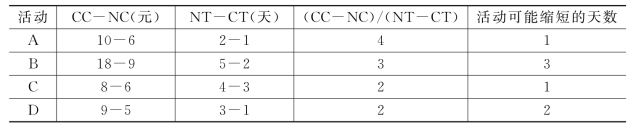
（3）计算关键路径。注意，此时我们需以正常时间为基础计算项目的关键路径。该网络图较为简单，可得出关键路径为A-B-D，初始工期为10天。

（4）在费用增加最小的前提下缩短关键路径的完工时间。最简单的办法是将关键路径上赶工费用率最低的活动的完成时间减少一天，然后重新计算并寻找新的关键路径，在新的关键路径上同样逐日减少完工时间。重复这一步骤，直到获得满意的完工时间或完工时间不能再缩短为止。表7-3例示了这一过程。

表7-3　项目活动分解和定义的主要工作

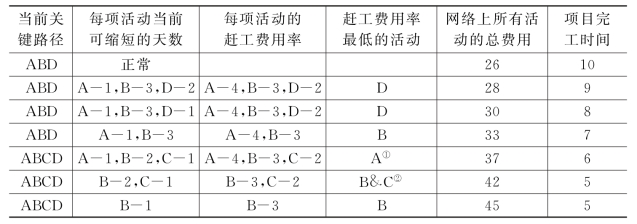
注：①为减少关键路径总完成时间一天，缩短活动A的时间一天，或同时缩短B和C的时间（B或C单独缩短工期都只能修改一条关键路径，而不能缩短总完工时间）。
②B和C必须一起压缩才能缩短关键路径工期一天。

（5）作出直接费用、间接费用和总费用曲线，以制定最小费用计划，如图7-9所示。

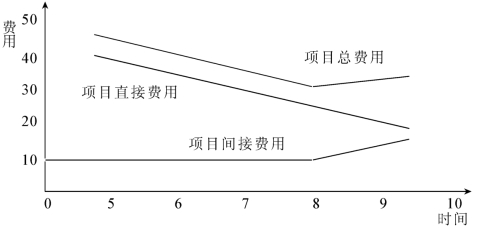
图7-9　寻找总成本最小的时间点

上图中，间接费用曲线前8天每天费用为10元，以后每天增加5元，直接费用曲线由图7-9获得，项目的总费用是这两个费用之和。由该图可以看出，总费用曲线的最小值是工期为8天的计划。