当一个项目的活动历时估计受到影响的因素比较少，或者我们能比较有把握地估计出各项活动的持续时间时，就可以对各活动只估计一个时间。在这种情况下，我们在推算整个项目的工期时，就可以利用关键路线技术（CPM）进行估算。下面我们将举例来说明如何基于单点时间估计推算项目工期。

例1：表6-3列出了一个简单的项目网络的数据。图6-9是我们根据该表画出的节点图。网络中包含的虚活动代表该网络的唯一起点。

表6-3　关键路线技术示例项目的数据分析

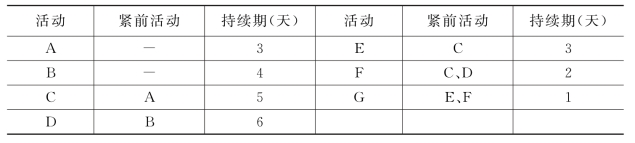
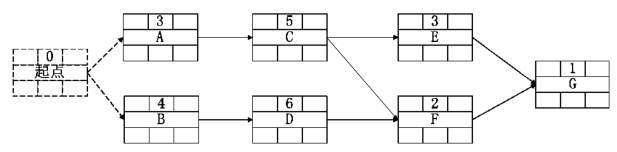
图6-9　附有活动持续时间的节点网络示例图

1.首先利用正推法求解关键路径并得出项目的工期

我们首先计算网络中所有活动的最早开始时间和最早结束时间。根据规则1，起始节点（虚活动）的最早开始时间为0，则最早结束时间也为0。由于活动A只有一个紧前活动，所以活动A的最早开始时间为ES（A）=EF（起点）=0。根据规则3，活动A的最早结束时间为EF（A）=ES（A）+t A=0+3=3。利用同样的方法可以求出节点B、C、D、E的最早开始时间和结束时间。而F、G和其他节点不同的是，它们都有超过一个的紧前活动。这时就要利用到规则2，我们以F节点为例，该节点的最早开始时间ES（F）=max（EF（C），EF（D））=max（8，10）=10。通过这样的计算我们得到附有活动最早开始时间和最早结束时间的节点网络示例图。如图6-10所示。

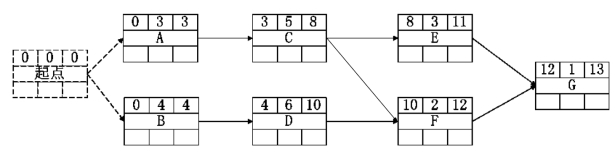
图6-10　附有活动最早开始时间和最早结束时间的节点网络示例图

根据规则8，我们知道起点和终点G都在关键路线上，同时我们可以从节点G逆推出关键路线。比如，现在已经确定节点G是关键活动，那么，我们开始比较活动G的最早开始时间和活动G的紧前活动E和F的最早结束时间，从图6-9可知，活动F才是关键活动。不断利用这一规则，我们最后求出关键路线为：起点→B→D→F→G。用图6-11表示（其中加粗的箭线表示关键路线）。

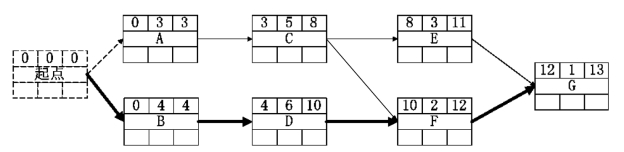
图6-11　正推法分析得出的标志关键路线的节点网络示例图

这样我们根据规则4就可以确定该项目的最早结束时间即最后一个活动G的最早结束时间为13天。

2.利用逆推法求解关键路线并得出项目的工期

首先我们通过项目的结束时间从最后一个节点反推向计算网络图中每一个节点的最迟开始时间（LS）和最迟结束时间（LF）。由于在此例子中，我们没有特别规定确定的最后期限，根据规则5，我们假定项目的最迟结束时间与最早结束时间相等，也即LF（项目）=EF（项目）EF（G）=13，则LS（G）=LF（G）-t G=12。如果某个活动i只有一个最邻近的后续活动j，那么活动i的最迟结束时间就等于活动j的最迟开始时间，例如活动E只有一个最邻近后续活动G，则LF（E）=LS（G）=12；如果活动i有多个后续活动，那么我们就可以根据规则6计算出该活动的最迟结束时间，比如活动C有两个最邻近后续活动，则LF（C）=min（9，10）=10；根据计算出来的最迟结束时间，再根据规则7可计算出最迟开始时间。这样我们通过逆推计算得到附有活动的最迟开始时间和最迟结束时间的节点网络示例图。如图6-12所示。

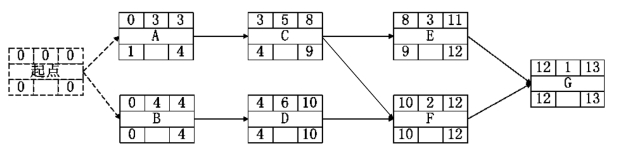
图6-12　附有活动最迟开始时间和最迟结束时间的节点网络示例图

现在我们利用计算总时差值的任意一个公式可以把每个活动的总时差计算出来。我们把计算结果在表6-4中列出，从表中可以看出以下节点的总时差均为0：起点、B、D、F、G，把它们依次连接起来就形成了自始至终的一条路线，所以这些点都是关键活动，这条路线就是关键路线。我们用图6-13进行表示（其中加粗的箭线则表示关键路线）。

表6-4　示例项目的关键路线分析结果

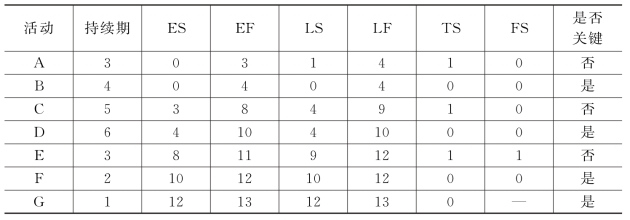
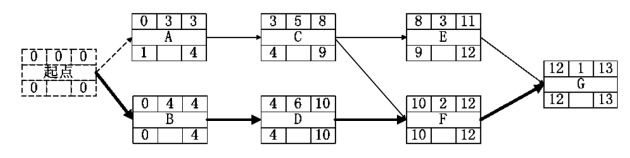
图6-13　逆推法分析出的标志关键路线的节点网络示例图

通过这个例子，我们还需要提醒读者注意两种时差。

●总时差（TS，Total Slack）(www.daowen.com)

总时差是指在不推迟项目最迟结束时间的前提下，一项活动可能的最早开始时间的推迟时间量。活动i的总时差就是该活动的最迟结束时间与最早结束时间之差，或者是该活动的最迟开始时间与最早开始时间之差。即：

TS（i）=LF（i）-EF（i），或TS（i）=LS（i）-ES（i）

●自由时差（FS，Free Slack）

自由时差是指在不推迟一项活动的任何最邻近后续活动的最早开始时间的前提下，其可能的最早开始时间的推迟时间量。活动i的自由时差等于该活动的最邻近后续活动j的最早开始时间与该活动的最早结束时间的差值的最小值。即：

其中，S（i）={活动i的最邻近后续行动}。

从以上定义我们可以看出，一个活动的总时差和自由时差是不一样的，总时差实际上是属于整条路线的，而不是活动本身，而自由时差只属于活动本身。这里需要注意到的是，总时差是一种非常危险的时差。为了证明这一点我们根据表6-4，假设活动C的负责人决定利用1个时段的总时差出去逛街。因此，他在时刻9这一可接受的最迟结束时间完成了活动C。当负责E活动的人出场时，如果他觉得他也有1个时段的总时差去做自己的事，等他在时刻10（9+1）返回时，工作正式开始并持续3天于时刻13完成，这时实际上已经造成了结束活动的停滞，延误了项目完成的时间。

由此我们得出一个结论：总时差属于整条路线，可以在路径上的不同活动间进行分配，但绝不能多次重复使用。而自由时差属于活动本身。事实上，上面的活动C不能被延误因为它的自由时差为0（它最早在时刻8结束，而后一个活动最早在时刻8开始），而活动E可以在不影响后续活动G的情况下延迟1个时段进行（它最早在时刻11结束，而后一个活动最早在时刻12才开始）。

在这里我们想给读者一个建议：无论在什么情况下，任何时差都要视为是项目经理的，而不是某个个人的。项目团队成员应该坚持以最早开始时间和最早结束时间为准则进行工作，这样不仅能使项目不容易延误，而且也能使项目不致落入帕金森（Parkinson）法则。该法则说的是：工作总是要拖到规定的截止时间才会完成。

例2：某公司正在进行一个ERP项目建设，由于项目组的人员对该项目的实施比较了解，他们对自己分配的任务比较熟悉，能比较准确地估计出各活动的历时，所以他们决定采用CPM方法来推算整个项目的工期。

（1）根据上一阶段项目活动分解产生的活动目录，采用上一节中活动历时估计的一些方法对各项活动进行历时估计，得到更新的活动目录表。如表6-5所示。

表6-5　某公司ERP项目活动目录表

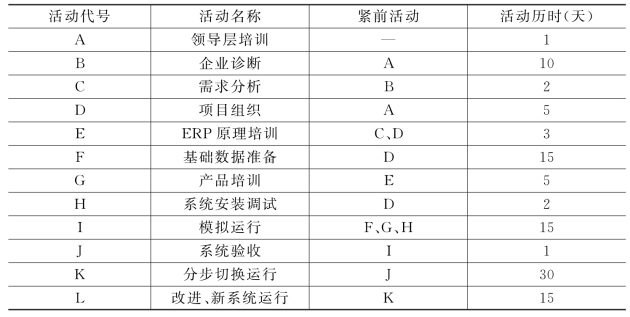
（2）根据表6-5绘制CPM节点网络图。注意确保活动顺序的正确性，同时还必须保证活动之间的逻辑关系。初始网络图如图6-14所示。

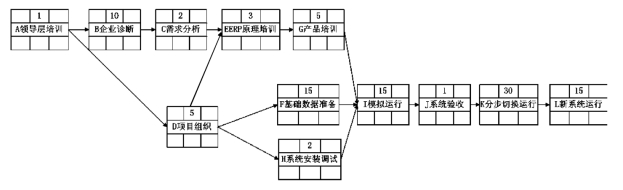
图6-14　初始节点网络图

（3）利用正推法确定关键路线。首先根据前边介绍的规则和公式计算出各项活动的最早开始时间（ES）和最早结束时间（EF），然后更新初始网络图。更新后的网络图如图6-15所示。

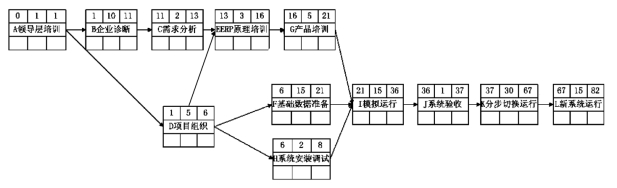
图6-15　更新节点网络图

（4）根据关键路径的确定原则，我们可以确定出该项目的关键路线，即以下两条：

第一条：A—＞B—＞C—＞E—＞G—＞I—＞J—＞K—＞L

第二条：A—＞D—＞F—＞I—＞J—＞K—＞L

我们可以知道该项目的估算工期为82天。由于该项目有两条关键路线，此时项目经理就需要对两条路线上的活动同时给予关注。

需要注意的是，项目总是处于一个变化的环境中，许多因素都影响着实际的活动时间，我们虽然找出了关键路线，估算出了项目的工期，这只是第一步。我们需要随着项目的进展，对网络图进行更新，此时可能会发生关键路线的改变。比如说活动F准备基础数据提前完成了，此时的关键路线就只剩下第一条了，可能就得加强对活动“ERP原理培训和产品培训”的关注，以免拖延项目的工期。