（一）关键路径法（CPM）

1.关键路径法的来历

关键路径法（CPM，Critical Path Method）是由雷明顿-兰德公司（Remington-Rand）的J.E.克里（J.E.Kelly）和杜邦公司的M.R.沃尔克（M.R.Walker）在1957年提出的，当时是为了帮助一个化工厂制定停机期间的维护计划而采用的。^[1]

以往在美国的工厂中，基于设备维护的要求，每年都必须安排一定的时间，停下生产线对机器设备进行全面维修，检修时间一般为125小时。1957年，美国路易斯维尔化工厂革新检修工作，把检修流程精细分解，凭经验估计出每个工作的时间，并按有向图建立起控制关系。他们惊奇地发现，在整个检修过程中不同路径上的总时间是有差别的，其中存在着最长的路径。通过反复压缩最长路径上的任务工期，最后只用了78个小时就完成了通常需要125小时完成的检修，节省时间达到38%，当年产生效益100多万美元。这就是著名的时间管理技术——关键路径法。^[2]这种工具现在也成了项目管理软件（包括微软项目管理软件Microsoft Project系列）使用的根本方法。

2.关键路径法的基本概念和基本规则

刚才我们从历史的角度介绍了关键路径法的基本情况，下面我们从技术的角度再对该方法进行阐述。该方法引入了一些很好的基本概念，以及在求解关键路径时需要用到的一些基本规则，在后面的例子中我们将不断用到这一节所介绍的基本概念和基本规则。

首先我们介绍该技术将用到的一些基本概念：

（1）最早开始时间和最早结束时间

最早开始时间（ES，Earliest Start Time）是指某项活动能够开始的最早时间，最早结束时间（EF，Earliest Finish Time）是指某项活动能够完成的最早时间。我们同时约定，最早结束时间等于最早开始时间加上该活动的估算时间，即EF=ES+该活动的时间估计值。

在整个项目的活动中，一个活动的最早开始时间依赖于（除了它没有紧前活动）其所有紧前活动的结束时间，这是由项目活动的排序结果所决定的。例如，生产家具，在把各个模块组装成整套家具之前必须把所需模块做完并准备好所需零件，如螺丝等。如图6-3所示。

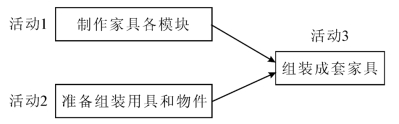
图6-3　组装家具活动关系示例

如果我们采用严格的结束-开始依赖关系，前一项活动任务没有全部完成，后一项活动显然就无法开始。因此，某项活动的最早开始时间取决于前一项活动的最早结束时间，它必须晚于或与前一项活动的最早结束时间相同。但是，为了保证项目能如期完成，我们还常常需要知道每项活动最迟不得晚于某一时间必须结束，这也就是下面我们将要介绍的最迟时间系列。

（2）最迟开始时间和最迟结束时间

最迟开始时间（LS，Latest Start Time）是指为了使项目在完工时间内完成，某项活动最迟必须在什么时候开始；最迟结束时间（Latest Finish Time，简称LF）是指为了使项目在要求完工的时间内完成，某项活动最迟必须在什么时候结束。最迟开始时间，可以用该项活动的最迟结束时间减去该活动的估算时间来得到，即LS=LF-活动的时间估计值。

由于项目活动的关联性，一个活动的开始时间、结束时间决定着下一个活动的开始时间、结束时间。在上面的生产家具的例子中，组装成套家具（活动3）的最早开始时间最早也要等到制作家具各模块（活动1）和准备好组装工具与物件（活动2）都完成；反之，活动1和活动2的最迟结束时间也不得晚于活动3的最迟开始时间。

（3）总时差（TS，Total Slack）

如果最迟开始时间与最早开始时间不同，那么该活动的开始时间就可以浮动，称之为存在时差（Float or Slack）；同理，如果最迟结束时间与最早结束时间不同，那么该活动的结束时间也可以浮动，同样称之为存在时差。总时差是指在不推迟整个项目的最迟结束时间的前提下，一项活动可能的最早开始时间的推迟时间量。对同一活动来说，以下两个公式计算出来的总时差值是相等的。即：

总时差（TS）=最迟开始时间（LS）-最早开始时间（ES）

总时差（TS）=最迟结束时间（LF）-最早结束时间（EF）

总时差可以用来确定项目的关键活动。

（4）正推法（Forward pass）

它是指按照网络逻辑关系从项目开始的那一刻正向（一般从左至右）对所有网络活动中未完成部分最早开始时间和最早结束时间的计算。如果某项活动只有一个紧前活动，那该项活动的最早开始时间为它的紧前活动的最早结束时间。如果某项活动有几个紧前活动，那该项活动的最早开始时间为这些紧前活动的最早结束时间的最大值。

图6-4是一个简单的网络图，每个圆圈中的英文字母代表活动名称，数字代表活动用时，每个圆圈上面的数字，左边的代表最早开始时间，右边的代表最早结束时间，以后我们不再特别注解，一律都是这个含义。如图6-4所示，A这项活动是整个项目的开始活动，没有紧前活动，我们将其ES规定为0（这纯粹是为了计算简便，实际上你可以使用任何一个数字，只要满足项目的具体要求，比如10，意味着第10天开始，或者2005.9.20，意味着2005年9月20日开始），自然它的EF就是0+2=2。活动B的紧前活动只有活动A，所以它的ES就是2（我们也假定活动之间不必交接、等待，紧跟着就可以结束和开始），而EF就是2+4=6。同理，活动C的ES是2，EF为8。那活动D的ES是多少呢?它有两个紧前活动，利用刚才介绍的原理，它的ES是其所有紧前活动的EF中最大的数值，本例中就是8，如果你写成6那就错了。这个例子提醒我们，在计算ES、EF时，如果遇到有箭头汇聚进来的活动，必须加以小心。

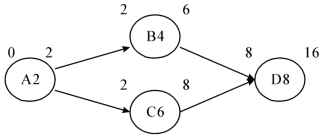
图6-4　组装家具活动关系示例

（5）逆推法（Backward Pass）

它是指按照网络逻辑关系从项目结束的那一刻反向（一般从右至左）计算网络中所有未完成活动的最迟开始时间和最迟结束时间的计算。如果某项活动只有一个紧后活动，那该项活动的最迟结束时间为它的紧后活动的最迟开始时间。如果某项活动有几个紧后活动，那该项活动的最迟结束时间为这些紧后活动的最迟开始时间的最小值。

项目结束时间可以是正推法计算所得到的结束时间或由客户或代理指定的结束时间。

如图6-5所示，活动D是整个项目的最后一项活动，没有紧后活动，我们将其LF规定为16（这也纯粹是为了计算简便，实际上你可以使用任何一个数字，只要满足项目的具体要求，比如20，意味着第20天结束就可以，或者2005.10.20，意味着2005年10月20日结束），它的LS就是16-8=8。活动D的紧前活动分别是活动B和活动C，所以它们的LF都是8（我们也假定活动之间不必交接、等待，紧跟着就可以结束和开始），而LS分别是4和2。那活动A的ES是多少呢?它有两个紧后活动，利用刚才介绍的原理，它的LF是其所有紧后活动的LS中最小的数值，本例中就是2，如果你写成4那就错了。这个例子提醒我们，在计算LS、LF时，如果遇到有箭头发散出来的活动，必须加以小心。

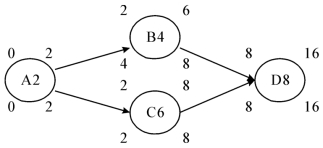
图6-5　组装家具活动关系示例

在经历了正推法计算和逆推法计算后，对于每个活动我们都得到了4个数据，即ES、EF、LS、LF，这是项目管理特有的计算方法，将为我们计算整个项目的工期和得到所有活动的进度信息提供极大的帮助。

（6）关键路径（Critical Path，也叫关键路线）

在项目网络图中，它是决定项目最早完成时间的路线。当某些活动超前和滞后于计划完成时，关键路线通常将随时间的变化而变化。虽然通常是计算整个项目的关键路线，但也可以确定达到一个里程碑或子项目的关键路线。通常按照总时差小于或等于某个确定的值（通常是0）的活动来确定关键路线。即所有LS-ES或者LF-EF等于零的活动，如果能从头串到尾，就是关键路径。故一个项目可以存在多条关键路径。在我们刚才举的例子中，A、C、D符合这样的要求，所以它就是这个项目的关键路径。它是整个项目中所有路径中耗费时间最长的，却决定着项目能够完工的最短时间。

（7）关键活动（Critical Activity）

它是处于关键路线上的所有活动。从另一个角度来说，关键活动是指那些在网络图中总时差量最小的活动。要注意的是，如果项目的最后期限没有明确规定，则该活动的总时差为0。需要注意，我们这里使用的“关键”并没有别的含义，那些耗费资金比较大的活动，那些从来没有干过而风险又比较大的活动，那些耗费时间最长的活动，在你的心目中可能都很关键，但它们不是我们这里所说的关键活动。

以前我们曾说过，AON网络图（节点表示活动，也叫节点图）除了用圆圈来表示节点外，还可以用方框来表示，如图6-6所示。其好处就是可以集中标出节点所代表的活动名称、最早开始时间、最早结束时间、最迟开始时间、最迟结束时间以及活动持续时间。信息既全面，又整齐美观。

图6-6　以方框表示节点示例

我们在本书中基本都使用AON法。因为它简洁清晰，也被广泛用于大部分流行的项目管理软件中。节点图表示法的一个优点是其网络图很容易手工绘制。而AOA法（箭线图），当多于15或20个活动时，用手工画非常难，但用现代软件这也不是什么大问题。节点图通常不显示事件，但可以很容易地把事件（通常是里程碑）作为零历时和零资源的活动表示出来。

下面再集中将该技术用到的基本规则描述如下：

规则1

除非特别规定，不然一个项目的起始时间都定于时刻0。也就是说，网络图中的所有开始节点，其最早开始时间（ES）都是时刻0。如果只有一个开始节点，那么，ES（1）=0。如果假定开始时间是一个具体的时刻t0，那么，ES（1）=t0。

规则2

任何活动节点j的最早开始时间（ES）等于其紧前活动节点i的最早结束时间（EF）的最大值，则：

其中，p（j）={活动j的紧前活动}。

规则3

活动i的最早结束时间（EF）是该活动的最早开始时间与该活动持续时间的估计值ti的和，则：

EF（i）=ES（i）+t i

规则4

项目的最早结束时间等于项目网络中最后一个节点（假设为节点n）的最早结束时间。因此，EF（项目）=EF（n）。

规则5

除非项目的最迟结束时间明确规定，不然按照惯例，我们将其定为项目的最早结束时间。因此，LF（项目）=EF（项目）。如果项目的最迟结束时间规定为tp，那么，LF（项目）=tp。

一般情况下，对于一个基于合同的项目，最迟结束时间通常也是确定的。但在计划评审技术中，我们用最早结束时间来代表项目的估算工期，依此可以算出各种假设的完工期限的完工概率。

规则6

活动i的最迟结束时间（LF）是该活动紧后活动j的最迟开始时间（LS）的最小值，则：

其中，S（i）={活动i的紧后活动}。

规则7

活动i的最迟开始时间是其最迟结束时间与该活动持续时间的估算值之差。因此，LS（i）=LF（i）-ti。

规则8(www.daowen.com)

假设活动j有一个紧前活动i，并且活动j确定为关键活动，此时我们比较EFi和ESj。如果EFi=ESj，那么，就将活动i标为关键活动。

规则9

如果网络中只有单一的起点或者单一的终点，那么，该节点一定在关键路线上，即该节点属于关键活动。

（二）计划评审技术（PERT）

在项目资源配置确认之前，项目工期计划只是初步计划；在项目资源配置得到确认以后，才能够得到正式的项目工期计划。

项目工期计划文件可以使用摘要的文字描述形式给出，也可以使用图表的形式给出。

1.计划评审技术（PERT）的基本概况

在关键路线法发明一年以后，美国海军开始研制北极星导弹。这是一个军事项目，技术新，项目规模巨大，共有3000多个承包商和研究机构参加开发，据说当时美国有1/3的科学家都参与了这项工作。管理这样一个项目的难度可想而知。而当时的美国海军部武器局的特别计划室、博思管理顾问公司（Booz-Allen Hamilton）和洛克希德飞机公司（后来的洛克希德·马丁公司）共同研究出了一个方法，即计划评审技术（Program Evaluation and Review Technique，简称PERT）。其理论基础是假设项目活动持续时间以及整个项目完成时间是随机的，且服从某种概率分布，这样利用PERT就可以估计整个项目在某个时间内完成的概率。

PERT与CPM一样，在项目的进度规划中应用非常广。PERT的形式与CPM网络计划基本相同，只是在活动持续时间方面CPM仅使用一个确定的工作时间；而PERT要用到三个时间估计，一般称作乐观的时间估计值a、最可能的时间估计值m及悲观的时间估计值b，然后按照β分布计算各项活动的期望时间t。最后竟然只用了4年的时间就完成了预定6年的项目，节省时间达到了33%以上，使北极星导弹的研制工作在时间（提前两年）和成本控制方面取得显著效果。因此，美国三军和航空航天局决定在各自管辖的计划工作中全面推广这项技术。如1962年美国国防部规定：凡承包有关工程的单位都需要采用这种方法来安排计划。后来，有42万人参加的耗资400亿美元的“阿波罗”载人登月计划，也是利用这种方法进行计划、组织与管理的。当今提起PERT（有时称为网络图）就是指这种表示任务关系图形的方法。

2.PERT的基本公式和参数

PERT可以视为是关键路径法的延伸，它将活动持续时间视作随机变量，并将这种考虑加入到项目的网络分析中。

在现实中，项目会经常受到一些不确定因素的影响。在关键路径法中，假定活动持续时间是确定不变的。PERT通过对每种活动使用3种时间估计来解决活动持续期中存在的潜在不确定性。这3种时间估计代表了活动持续期估计的范围。一项活动的不确定性越大，估计值的范围就越宽。

在3种时间估计的基础上，PERT通过使用简单的公式来计算每项活动的期望持续时间和方差。这套公式建立在β分布的均值和方差基础上。均值的近似公式是3个时间估计的简单加权平均值。同时，PERT的近似公式基于这样一种认识，即一个分布的大多数观察值落在正负3倍标准差之内，或者说其变化幅度只限于6倍的标准差。这样，我们就得到了一种简单方法，即将PERT公式的标准差设定为等于持续范围估计值的1/6，因此得到公式：

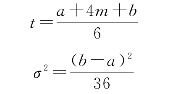
其中，a为乐观的时间估计值，m为最可能的时间估计值，b为悲观的时间估计值（a＜m＜b）；t为活动持续时间的期望值，σ2为活动持续时间的方差。

3.相关数理方面的基础知识

（1）正态分布

通过标准正态分布来计算随机变量在某个区间内的概率是非常容易的。标准正态分布即数学期望EX为0，而方差DX为1。标准正态随机变量Z与一般正态分布的随机变量X的关系如下：

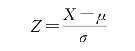
其中，μ和σ为随机变量X的数学期望和标准差。这样求X在某个区间内的概率就可以转换为标准正态分布Z在某个区间内的概率，通过正态分布表就可查出。例如：

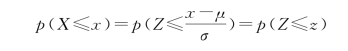
此时的概率就为标准正态分布曲线下z左边图形的面积。图6-7给出了形象的表示。

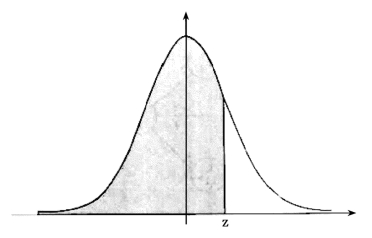
图6-7　标准正态分布曲线下的面积

（2）中心极限定理

中心极限定理指出，如果样本量足够大并且相互独立，那么从任何概率密度函数得到的平均值的分布都近似为正态分布。在数学中，中心极限定理陈述如下：独立同分布随机变量之和的极限分布是正态分布。

具体说，假定X1，X2，…，XN为独立同分布的随机变量序列，那么，当N充分大时，这些随机变量的和TN的分布近似服从正态分布。这个和定义为：

T N=X 1+X 2+…+X N

在活动网络分析中，TN代表关键路线上活动持续时间总和所确定的项目总工期。T的均值和方差表示为：

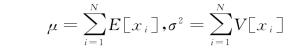
其中，E[xi]为随机变量xi的期望值；V[xi]为随机变量xi的方差。

从上面的定理可以看出，该定理要成立的一个必要条件是这些随机变量要有相同的概率分布且互相独立。但在实际项目当中，由于各活动间的优先顺序关系和其他相互依赖性，所以一些活动持续时间并不是互相独立的。为了便于计算我们假定各活动持续时间为互相独立，从而把中心极限定理应用于活动网络。这正如PERT技术把活动持续时间的分布看成是β分布一样，虽然活动时间的真实分布从来都是未知的。当然也有一些学者避开活动持续时间的独立性，从另一个角度来估计项目工期的完工概率，有兴趣的读者可以阅读一下这方面的深入研究。^[3]

4.PERT计划评审技术应用举例

在下面提到的这个例子中，我们要给每个活动三个持续时间的估计值，然后利用上面的基本公式计算出每个活动持续时间的均值和方差。我们把该例子拥有的项目数据列在表6-1中。表的右面两列给出的就是使用PERT基本公式算出的活动持续时间的期望值和方差。

表6-1　附有活动持续时间期望值和方差的PERT项目数据

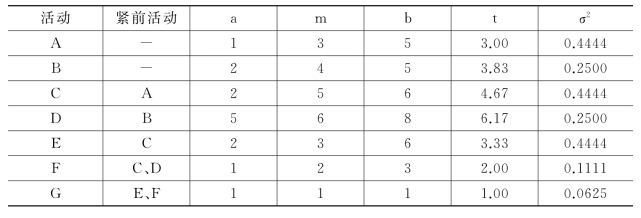
利用关键路线法和表6-1中的数据我们可求出该项目的关键路线，我们用图6-8表示该项目的PERT网络。如下所示。

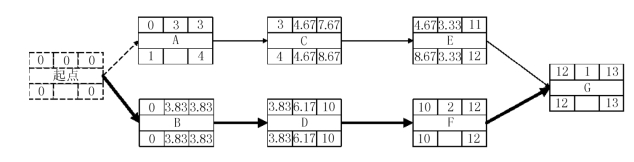
图6-8　基于期望工期的网络示例图

由上图我们可以知道，该项目的期望总工期TE=13，下面我们求关键路线上各关键工作的标准离差σ。其计算公式如下：

这样我们求得σ=0.8207。下面我们假设要问该项目在TD=11天内完工的概率有多大。根据前面的中心极限定理和正态分布，我们可以得出以下计算式：

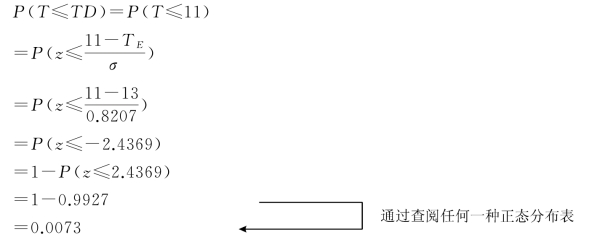
也就是说，该项目要在11天内完工的概率为0.73%，几乎是不可能的。进一步，如果要问该项目在TD=15天内完工的概率是多少，则：

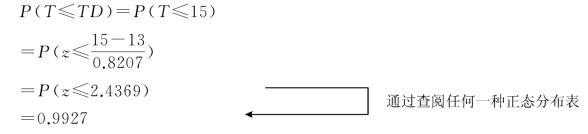
这也就意味着该项目在15天内的完工概率超过了99%，几乎是十拿九稳。

为了便于读者能更深刻地体会完工概率的计算方法，我们模拟几组数据，得出在不同的最后期限下的完工概率，如表6-2所示。

表6-2　不同最后期限的完工概率计算表

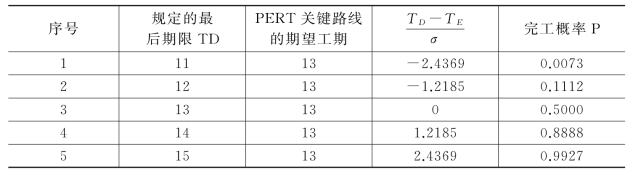
小提醒:以上的完工概率我们都是指在规定的某个期限内完成项目的概率，但如果是求恰好在某一天完成项目的概率呢?这里的答案是0。比如说项目恰好在第15天完成的概率则为0。因为我们这里的假设是项目的总工期服从正态分布，从数学角度讲，这是一种连续型概率分布。而连续型随机变量取任何给定值C的概率等于0。从实际角度讲，要求项目在某个时点上刚好圆满完成也几乎是不可能的任务。

（三）仿真（蒙特卡罗方法）

除了上述两种方法以外，还有一些仿真方法来估计项目的工期，在此我们只作一简单介绍。

仿真就是用不同的假设来计算相应的时间，最常见的是蒙特卡罗方法。在这种方法中，假设了各活动所用时间的概率分布以用来计算整个项目完成所需时间的概率分布。

蒙特卡罗方法是一种计算方法，它与一般数值计算方法有很大区别。它是以概率统计理论为基础的一种方法。由于蒙特卡罗方法能够比较逼真地描述事物的特点及演变过程，解决一些数值方法难以解决的问题，因而该方法的应用领域日趋广泛。下面以一例子（射击游戏）来说明。

设r表示射击运动员的弹着点到靶心的距离，g（r）表示击中r处相应的得分数（环数），f（r）为该运动员的弹着点的分布密度函数，它反映运动员的射击水平。该运动员的射击成绩为：

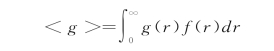
用概率语言来说，＜g＞是随机变量g（r）的数学期望，即：

＜g＞=E[g（r）]

由以上例子可以看出，当所求问题的解是某个事件的概率，或者是某个随机变量的数学期望，或者是与概率、数学期望有关的量时，通过某种试验的方法，得出该事件发生的频率，或者该随机变量若干个具体观察值的算术平均值，以此得到问题的解，这就是蒙特卡罗方法的基本思想。

通过某种试验，得到N个观察值r1，r2，…，r N（用概率语言来说，从分布密度函数f（r）中抽取N个子样r1，r2，…，r N），将相应的N个随机变量的值g（r1），g（r2），…，g（r N）的算术平均值作为积分的估计值（近似值）。

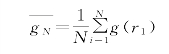
为了得到具有一定精确度的近似解，所需试验的次数是很多的，通过人工方法作大量的试验相当困难，甚至是不可能的。因此，蒙特卡罗方法的基本思想虽然早已被人们提出，却很少被使用。20世纪40年代以来，由于电子计算机的出现，使得人们可以通过电子计算机来模拟随机试验过程，把巨大数目的随机试验交由计算机完成，使得蒙特卡罗方法得以广泛地应用，在现代化的科学技术中发挥了巨大的作用。