假定社会生产使用两种要素，这两种要素分别为L和K，其既定数量为L-和K-；社会中存在两个生产者，这两个生产者分别为C和D。

同样运用埃奇渥斯盒状图分析要素L和K在生产者C和D之间的分配状况，如图11-3所示。

图11-3　生产的帕累托最优

盒子的水平长度表示整个经济中第一种要素L的数量L-，盒子的垂直高度表示第二种要素K的数量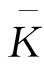。OC为第一个生产者C的原点，OD为第二个生产者D的原点。从OC水平向右测量生产者C对第一种要素的生产消费量LC，垂直向上测量它对第二种要素的生产消费量KC；从OD水平向左测量生产者D对第一种要素L的生产消费量LD，垂直向下测量它对第二种要素K的生产消费量KD。显然，盒中任意一点（包括边界）确定了两种生产要素在两个生产者之间所有可能的分配情况，即盒中任意一点都表示任一生产者对两种生产要素的生产消费量的组合，因而有

在埃奇渥斯盒中，有两个生产者的等产量线。一方面，由于OC是生产者C的原点，故C的等产量线如ⅠC、ⅡC和ⅢC所示，其中ⅢC代表较高的产量水平，ⅠC代表较低的产量水平。一般来说，从OC向右移动，表示生产者C的产量水平增加。另一方面，由于OD是生产者D的原点，故D的等产量线如ⅠD、ⅡD和ⅢD所示，其中ⅢD代表较高的产量水平，ⅠD代表较低的产量水平，一般来说，从OD点向左移动，表示生产者D的产量水平增加。(www.daowen.com)

埃奇渥斯盒中的a′点是生产者C的等产量线ⅡC和生产者D的等产量线ⅠD的交点。若改变a′点的分配状态，比如让a′点变动到b′点，则生产者C的产量水平从等产量线ⅡC、提高到ⅢC，而生产者D的产量未变化，仍然是等产量线ⅠD表示的产量。因此，a′点存在着帕累托改进的余地。若让a′点变动到c′点，则生产者C的产量未提高，但生产者D的产量增加了；如果让a′点变动到d′点，则生产者C和D的产量都增加了。由此得到结论：在生产的埃奇渥斯盒状图中的任意一点，如果它处在生产者C和D的两条等产量线的交点上，则它就不是帕累托最优状态。

另外，如果要素分配状态处于两条等产量线的切点如c′点（c′点是生产者C的等产量线ⅡC与生产者D的等产量线ⅡD的切点），则容易看出此时不存在任何帕累托改进的余地，即c′点为帕累托最优状态。原因在于：c′点若向右上方移到生产者C较高的等产量线上，则生产者D的产量会下降；c′点若向左下方移到生产者D较高的等产量线上，则生产者C的产量水平会下降；若从c′点移到g′点和f′点，则生产者C和D的产量水平都降低。由此可得出结论：在生产的埃奇渥斯盒状图中的任意一点，如果它处在生产者C和D的两条等产量线的切点上，则它就是帕累托最优状态，并称之为生产的帕累托最优状态。

等产量线的切点不只是c′点一个，b′点和e′点等也都是等产量线的切点，从而也都是帕累托最优状态。所有等产量线的切点的轨迹构成曲线qq′。qq′曲线叫作生产的契约曲线（或效率曲线），它表示两种要素在两个生产者之间的所有最优分配（即帕累托最优）状态的集合。

与交换的契约曲线一样，在生产的契约曲线上即在生产的帕累托最优集合中，两个生产者的福利分配也具有不同的情况。当沿着qq′曲线从e′点移到c′点时，生产者C通过牺牲生产者D的利益而好起来，反之亦然。根据帕累托标准，这些最优分配组合是不可比较的。只能说，给定任何不在曲线qq′上的点，总存在比它更好的点，而这些点在曲线qq′上。

生产的帕累托最优状态是等产量线的切点，而等产量线切点的条件是，在该点上两条等产量线的斜率相等。由于等产量线斜率的绝对值叫作两种要素的边际技术替代率，因此，生产的帕累托最优状态的条件可以表示为：要使两种要素L和K在两个生产者C和D之间的分配达到帕累托最优状态，则对于这两个生产者来说，这两种要素的边际技术替代率必须相等。假如对于生产者C和D来说，L代替K的边际技术替代率分别用和来表示，则生产的帕累托最优状态条件就是