洛伦茨曲线由美国统计学家M.O.洛伦茨于1905年提出，是用来分析全部收入在获得这些收入的全体社会成员之间分配均等状况的曲线，也就是用来衡量全社会收入分配平均程度的曲线。洛伦茨曲线的具体做法如下。

第一步，按照经济社会成员的收入由低到高的顺序进行分组。

第二步，统计经济中收入最低的10%的人群的总收入在整个经济的总收入中所占的比例，再统计经济中收入最低的20%的人群的总收入在整个经济的总收入中所占的比例，以此类推。注意：这里的人口百分比和收入百分比在统计时都是累积百分比。

第三步，将得到的人口累积百分比和收入累积百分比的统计数据投影在图6-9中，得到一系列的点，将这一系列的点用平滑的曲线联结得到一条曲线，即图中的ODY曲线，这条曲线就是洛伦茨曲线。(www.daowen.com)

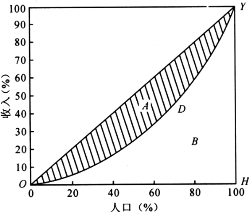
图6-9　洛伦茨曲线

图6-9中的对角线OY具有特殊的含义，因为OY是45°线，在这条线上横坐标与纵坐标相等，即经济中收入最低的10%的人口得到社会10%的收入，收入最低的20%的人口得到社会总收入的20%，以此类推，也就是人口累积百分比等于收入累积百分比，因此OY表示了经济社会中每个成员得到了同样比例的收入，因而OY又被称为绝对平均线。而折线OHY则表示了相反的收入分配状况，它意味着经济中极少数的人得到了社会100%的收入，因而这条线又叫作绝对不平均线。一个国家的收入分配状况既非绝对平均，又非绝对不平均，因而实际的洛伦茨曲线位于绝对平均线与绝对不平均线之间。洛伦茨曲线将OYH三角形分成了两部分，一部分为A，另一部分为B。显然A的面积越小，洛伦茨曲线与绝对平均线越接近，说明收入分配越平均；A的面积越大，即洛伦茨曲线弯曲的弧度越大，它与绝对不平均线越接近，它所代表的收入分配就越不平均。

利用上述方法可以比较同一个国家在不同时期的洛伦茨曲线或比较同一时期不同国家的洛伦茨曲线，通过不同的洛伦茨曲线的位置变化来判断收入分配平均状况和变化状况。