古诺模型是法国数理经济学家古诺（Augustin Curnot）在1838年出版的《财富理论的数学原理研究》一书中首次提出的寡头垄断模型。古诺分析了两个生产成本为零的出售同质的矿泉水的厂商。这两个厂商产品的边际成本都为零。它们面临相同的线性需求曲线，采用同样的市场价格出售产品，各厂商将它的竞争者的产量水平当作固定的，然后决定自己生产多少。在此假设下，古诺认为，两个厂商都会根据利润最大化原则不断地调整产量，直到各自的产销量正好等于市场为完全竞争市场时矿泉水产销量的1/3。

古诺模型可以用图5-14说明。图中DB为矿泉水市场的需求曲线或平均收益曲线，DQ1为边际收益曲线，边际成本MC为零。假定需求曲线DB决定的全部市场容量为OB=1200，开始时，唯一的产销者厂商A按照市场容量的半数提供产量，因为这时MR=MC=0，符合利润最大化的要求。OQ1对应的价格为OP1=6，成本为零，所以总利润为P1Q1=6×600=3600，在图5-14中表现为四边形OP1E1Q1的面积。

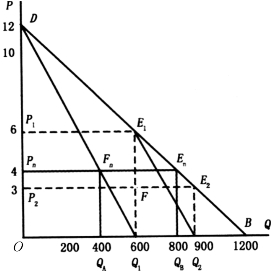
图5-14　古诺模型

接着市场上出现了厂商B，它以为厂商A不会改变产销量，把厂商A剩下的市场容量的半数Q1B=600作为自己的市场容量，和厂商A一样，为了实现利润最大化，厂商B按照剩下的市场容量的半数300]提供产量，这时对应的价格为OP2=3，厂商B获得P2·Q1Q2=3×300=900的利润，在图5-14中表现为四边形Q1FE2Q2的面积。

由于厂商B的介入，矿泉水的价格下降，厂商A的利润受到影响。为实现利润最大化，厂商A及时调整产量，把产量定为厂商B剩下的市场容量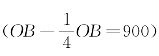的半数450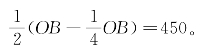，厂商A产销量的减少，导致价格上升，厂商B的市场容量扩大。厂商B也及时调整产量，按照厂商A剩下的市场容量的半数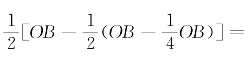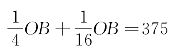确定产量。接着厂商A又会进一步减少产量。就这样，两家厂商从实现利润最大化目标出发，按照对方剩给自己的市场容量的半数不断地调整产销量，直到最后两家厂商的产销量各为市场容量的1/3，即为止。

厂商A产量调整的序列为：

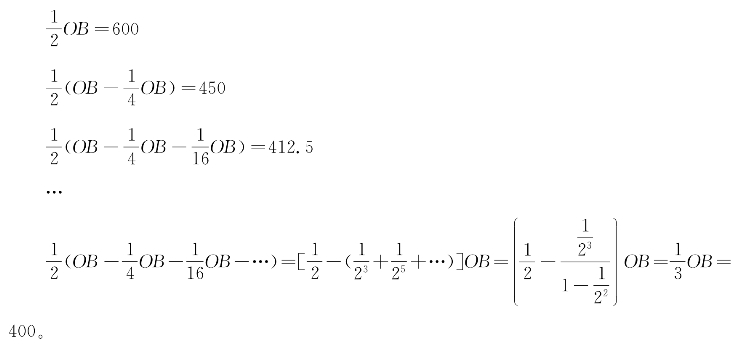
所以，厂商A的最终产量为400。

厂商B产量调整的序列为：

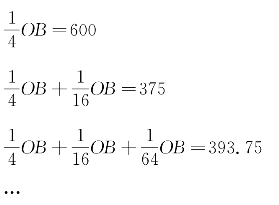
1

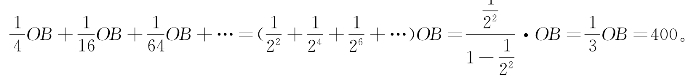
所以，厂商B的最终产量也为400。如图5-14所示，厂商A的产销量为OQA=400，厂商B的产销量为QAQB=400，市场价格为Pn=4。厂商A的利润为Pn·OQA=4×400=1600，在图5-14中表现为OPnFnQA的面积；厂商B的利润为Pn·QAQB=4×400=1600，在图5-14中表现为QAFnEnQB的面积；总利润为Pn·（OQA+QAQB）=4×（400+400）=3200，在图5-14中表现为OPnEnQB的面积，这就是古诺模型的结论。

古诺模型很容易被推广到一般，如果寡头垄断市场有n个企业，那么，厂商均衡的总产销量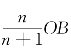，单个厂商的均衡产销量为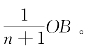若n=1，则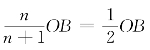，这是完全垄断厂商的均衡产量；若n为少数有限个厂商，则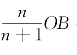代表寡头垄断市场所有厂商均衡时的总产量；若n为无穷大，则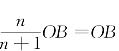，这是完全竞争市场厂商均衡时的总产量。随着n从1到无穷大的变化，市场的总产销量不断扩大，所以，寡头垄断的总产量大于完全垄断的总产量而小于完全竞争的总产量。

古诺模型还可用下面方法做进一步的说明。

从图5-14看，厂商A、B实际上面临的共同需求函数和成本函数分别为

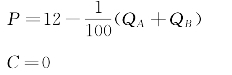(www.daowen.com)

因此，厂商A、B的利润函数分别为

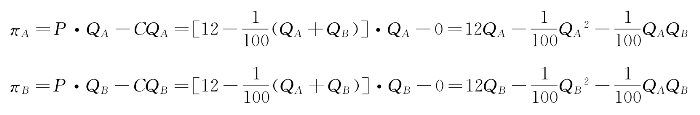
为使利润最大化，利润函数的一阶偏导应为零，即

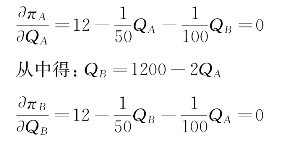
从中得：QA=1200-2QB

这两个式子，即

QA=600-和QB=600-分别被称为厂商B和厂商A的反应函数。

反应函数（Reaction Function）表明每个厂商的产量都是其竞争对手的产量的函数，具体来说，厂商1的利润最大化产量是他认为厂商2将生产的产量的减函数。一个厂商产量的增加会导致另一个厂商最优产量的下降。上述厂商A的反应函数表明对应于QB的任何特定值，QA是使πA最大化的产量；厂商B的反应函数表明对应于QA的任何特定值，QB是使πB最大化的产量。利润最大化的QA和QB的值，必须同时满足两个反应函数。

如果在直角坐标系中画出两个反应函数的曲线，如图5-15所示，两条反应函数曲线的交点H对应的QA和QB的值，则是两个厂商的均衡产量。

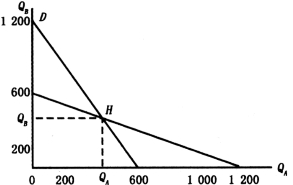
图5-15　反应曲线与古诺均衡点

QA=400

QB=400

代入需求函数

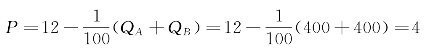
代入利润函数

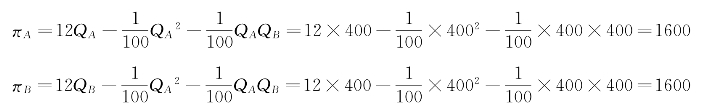
要注意的是：古诺模型的厂商的边际成本不一定要假设为零。这时，仍可根据上述方法求得两家厂商的产量、价格和利润。