上面讨论到了生产者的生产区域和生产的经济区域,这些都只表明理性生产者对生产投入的可选择范围,并没有解决最优选择问题。要解决生产要素的最优组合问题,必须将等产量曲线和等成本线结合起来。要素的最优组合可以是产量一定时成本最低的要素组合,也可以是成本一定时产量最高的要素组合。这两种情况的要素组合点表现在图形上,都是等成本线和等产量曲线相切的点。如图4-6所示的E点,就是成本一定时产量最高的要素组合点,也叫作生产者均衡点。
在图4-6中,Q1、Q2、Q3代表三条不同等产量曲线,K1L1代表生产者在一定资金成本约束下的等成本线。显然,生产者在此成本约束下不可能达到Q3的产量;生产者可以达到Q1的产量,如在A、B两点的生产,但这种生产不能使产量最大,不符合经济原则。沿着K1L1直线将A、B点向E点移动,就可以得到这一总成本水平上的最高产量。
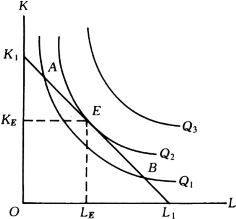
图4-6 成本一定产量最大的均衡
图4-7表示的是产量一定时,成本最小的要素组合。
在图4-7中,显然生产者只能选择K2L2成本线,低于K2L2的成本线,如K1L1,不能使生产达到Q的产量水平;高于K2L2的成本线,如K3L3,虽然可以生产Q产量,如A、B两点,但不经济;只有E点代表的KE和LE单位的资本与劳动的组合,才是生产Q产量最为节约,即成本最低的要素组合。
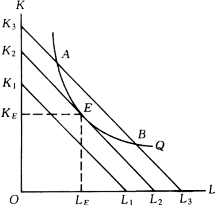
图4-7 产量一定成本最小的均衡
从以上分析可以看出,能满足要素投入最优组合的两个条件如下。(www.daowen.com)
(1)要素投入的最优组合处在等成本线上,这意味着厂商必须充分利用资金,而不让其剩余下来。
(2)要素投入的最优组合发生在等产量线和等成本线相切之点上,即要求等产量曲线的切线斜率与等成本线的斜率相等。
关于第二点,我们前面已知道,等产量曲线的斜率等于边际技术替代率,且为负数,等成本线的斜率是要素价格之比的负数,因此,PL/PK=MPL/MPK,即

上面的分析没有考虑生产要素价格变动对要素组合的影响。实际上,在生产要素可以相互替代的情况下,当其中某种生产要素的价格下降时,厂商会更多地使用这种生产要素,以替代别的生产要素。这种效应叫作生产要素的替代效应。同时,这种生产要素的价格下降,导致总成本下降,在收益不变的前提下,总成本的下降,会导致厂商增加产量,从而导致对这种生产要素使用量的增加。这种效应叫作生产要素的产量效应。这两种效应完全类似于第三章中讲到的替代效应和收入效应。
下面要介绍一下扩展线(expansion path)的概念。所谓扩展线,是代表不同产量水平的最优投入组合点的轨迹,如图4-8所示,E1、E2、E3分别表示当产量为Q1、Q2、Q3时的最佳投入组合。它们都是不同产量的等产量曲线与等成本线相切的切点,把这些切点联结起来所形成的曲线就是扩展线,它是生产函数和要素价格既定的生产扩展的路线,又称扩展轨道、规模曲线。
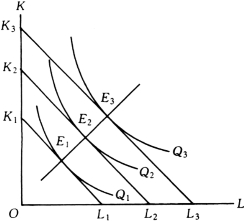
图4-8 生产扩展线
若已知生产函数Q=f(L,K)及要素价格PL和PK,则不难求得扩展线,方法是使边际技术替代率或两要素边际产量之比等于要素价格之比,即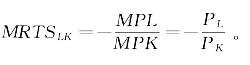
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







