短期生产函数研究的是一种可变配合比例的生产函数，即在假定其他投入不变，只有一种要素如劳动投入量可变的情况下，研究这种投入要素的最优使用量（即这种使用量能使企业利润最大）。为了探讨这个问题，需要从总产量、平均产量和边际产量这三个概念及其相互关系说起。总产量（Total Product）是指投入一定量的生产要素以后所得到的产出量总和，简称TP。平均产量（Average Product）是指平均每单位生产要素投入的产出量，简称AP。如果用L表示劳动投入量，那么

边际产量（Marginal Product）是指增加或减少1单位生产要素投入量所带来的产出量的变化，简称MP。

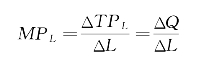
也可以写成

根据以上的定义公式，可以编制一种可变生产要素的生产函数的总产量、平均产量和边际产量的列表，表4-1就是一个例子。

表4-1　总产量、平均产量和边际产量

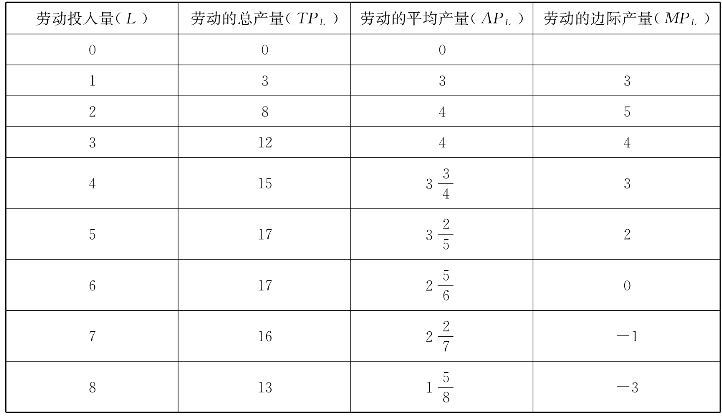
图4-1的横轴表示可变要素（劳动）的投入数量L，纵轴表示产量Q，TPL、APL和MPL三条曲线顺次表示劳动的总产量曲线、劳动的平均产量曲线和劳动的边际产量曲线。这三条曲线都是先呈上升趋势，然后达到本身的最大值，之后再呈下降趋势。

根据图4-1，可以从以下三个方面来分析这三条曲线相互间的关系。(www.daowen.com)

第一，关于总产量曲线和平均产量曲线之间的关系。由TPL曲线上任何一点，可以得到这一点上的相应的APL值。这是因为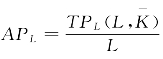，所以，联结TPL曲线上任何一点和坐标原点所得的射线，其斜率都可以表示为该点上的APL值。如图4-1中TPL曲线上A点所对应的APL值就是线段OA的斜率即，它等于A″L1的高度。

正是由于这种关系，当APL曲线在C′点达最大值时，TPL曲线必然有一条从坐标原点出发的最陡的切线，相切TPL曲线于相应的C点。

第二，关于总产量曲线和边际产量曲线之间的关系。由TPL曲线上任何一点，还可以得到这一点上相应的MPL的值。因为MPL=，所以，过TPL曲线上任何一点的切线的斜率，都可以表示为该点上的MPL值。如图4-1中过TPL曲线上A点切线的斜率，就是该点上的MPL值，它等于A′L1的高度。

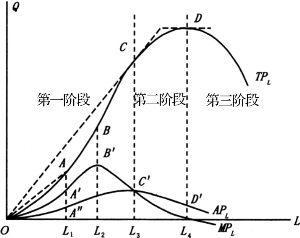
图4-1　TPL、APL、MPL曲线

当总产量在开始时随着劳动投入量的增加而增加时，TPL曲线的斜率为正，相应地，MPL为正值。当总产量随着劳动投入量的增加而减少时，TPL曲线的斜率为负，相应地，MPL为负值。以上这种关系也可以反过来说，只要边际产量是正的，总产量总是增加的；只要边际产量是负的，总产量总是减少的；当边际产量为零时，总产量达极值点（在此为最大值点）。

进一步讲，在总产量的上升段，随着劳动投入量的增加，当TPL曲线先以递增的速率增加时，MPL曲线随着TPL曲线的斜率的递增而上升。当TPL曲线的斜率在拐点B达最大值时，MPL曲线在B′点达最高点。当TPL曲线在B点以后以递减的速率继续增加时，MPL曲线在B′点以后随着TPL曲线的斜率的递减而下降。直至TPL曲线的斜率在D点降为零时，MPL曲线在D′点与水平轴相交。

第三，关于平均产量曲线和边际产量曲线之间的关系。图4-1中的APL曲线和MPL曲线之间的关系表现为：两条曲线相交于APL曲线的最高点C′。在C′点以前，MPL曲线高于APL曲线，MPL曲线将APL曲线拉上；在C′点以后，MPL曲线低于APL曲线，MPL曲线将APL曲线拉下。不管是上升还是下降，MPL曲线的变动都快于APL曲线的变动。

以上这些特征的原因在于：就任何一对平均量和边际量的一般关系而言，只要边际量大于平均量，边际量就把平均量拉上；只要边际量小于平均量，边际量就把平均量拉下。举一个例子：一个篮球队队员的平均身高为1.85米，如果新加入的一名队员的身高为1.90米（相当于边际量），那么整个队的平均身高就会增加。相反，如果新加入一名队员的身高为1.80米（相当于边际量），那么，整个队的平均身高会下降。因此，就平均产量APL和边际产量MPL来说，当MPL＞APL时，APL曲线是上升的；当MPL＜APL时，APL曲线是下降的。又因为MPL曲线是先升后降的，所以，当MPL曲线和APL曲线相交时，APL曲线必达最大值（可用数学方法证明）。

此外，在可变要素劳动投入量的变化过程中，边际产量的变动相对于平均产量的变动而言，要更敏感一些，所以，不管是增加还是减少，边际产量的变动都快于平均产量的变动。