无差异曲线和偏好这一概念是联系在一起的。无差异曲线是用来表示消费者偏好相同的两种商品的不同数量的各种组合。或者说，它是表示能给消费者带来同等效用水平或满足程度的两种商品的不同数量组合。与无差异曲线相对应的效用函数为

U=f（X1，X2）

其中，X1和X2分别为商品1和商品2的数量；U是常数，表示某个效用水平。由于无差异曲线表示的是序数效用，所以，这里的U只需表示某一个效用水平，而不在乎其具体数值的大小，有的西方学者称这种效用水平为效用指数。

无差异曲线可以用表3-3和图3-2来说明。表3-3是由某消费者关于商品1和商品2的一系列组合所构成的无差异表。该表由三个子表即表a、表b和表c组成，每一张子表中有商品1和商品2的不同数量的六种组合。每一张子表中的六种商品组合给该消费者所带来的效用水平被假设为是相等的。以其中的表a为例分析：表a中有商品1和商品2的A、B、C、D、E和F六种组合，A组合中有20单位的商品1和130单位的商品2，B组合中有30单位的商品1和60单位的商品2……消费者对于这六个消费组合的偏好程度是无差异的，他认为这六个组合各自给他所带来的满足程度是相同的。同样道理，消费者对表b中的六个商品组合的偏好程度也是无差异的，对表c中的六个商品组合给消费者带来的满足程度也是相同的。

表3-3　某消费者的无差异表

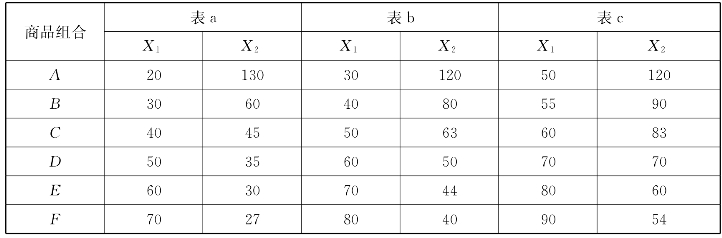
需要注意的是，尽管表a、表b和表c各自代表一定的效用水平，但是，它们之间的效用水平是不相同的。根据消费者偏好的第三个假设稍加分析就不难发现，表a所代表的效用水平低于表b，表b又低于表c。当然，消费者的偏好程度是无限多的，因此，他有无穷多个无差异子表，表3-3所表示的不过是其中的三个。

根据表3-3绘制的无差异曲线如图3-2所示。既然消费者具有无穷多个无差异子表，那么，根据无差异子表而画出的无差异曲线也有无数条，图3-2所表示的不过是其中的三条。

图中的横轴表示商品1的数量X1，纵轴表示商品2的数量X2，I1、I2和I3分别代表与表a、表b和表c相对应的三条无差异曲线。图中的无差异曲线是这样得到的：以无差异曲线I1为例，假定商品数量可以无限细分，先在坐标图上描出表a中的A、B、C、D、E和F的六个组合点，然后用曲线将这六个点连接起来，便形成了光滑的无差异曲线I1。与之类似，根据表b和表c，可以分别画出无差异曲线I2和I3。

图3-2中的每一条无差异线曲线上的任何一点，如无差异曲线I1上的A、B、C、D、E和F点所代表的商品组合给消费者带来的效用水平都是相等的。显然，无差异曲线是消费者偏好相同的两种商品的各种不同数量组合的轨迹。每一条无差异曲线代表一个效用水平，不同的无差异曲线代表不同的效用水平。在图3-2中，三条无差异曲线各自代表的效用水平是不相同的，其中，无差异曲线I3代表的效用水平大于无差异曲线I2，无差异曲线I2代表的效用水平大于无差异曲线I1。(www.daowen.com)

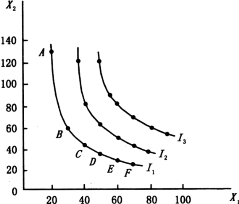
图3-2　某消费者的无差异曲线

无差异曲线具有以下的特点。

第一，由于通常假定效用函数具有连续性，于是，在同一坐标平面上的任何两条无差异曲线之间，存在着无数条无差异曲线。或者说，可以有无数条无差异曲线覆盖整个坐标平面图。离原点越近的无差异曲线代表的效用水平越低，离原点越远的无差异曲线代表的效用水平越高。在图3-2中，离原点最近的无差异曲线I1代表的效用水平最低，离原点最远的无差异曲线I3代表的效用水平最高，无差异曲线I2代表的效用水平居中。

第二，在同一坐标平面上的任意两条无差异曲线不会相交，这可以用图3-3来说明。

图3-3　违反偏好假定的无差异曲线

在图3-3中，两条无差异曲线I1和I2相交于A点。这说明无差异曲线I1上的B点的效用水平和无差异曲线I2上的C点的效用水平由于都等于相交点A点的效用水平，即消费者认为B点和C点是无差异的。但是，由于C点的商品组合所代表的两种商品的数量都大于B点的商品组合，根据消费者偏好的第三个假定，消费者对C点的商品组合的偏好必定大于对B点的商品组合的偏好。这样一来，消费者在认为B点和C点无差异的同时，又认为C点优于B点，这就违反了消费者偏好的第一个假定。所以，图3-3中两条无差异曲线相交的画法是错误的。

第三，无差异曲线是凸向原点的。从图3-2可见，无差异曲线不仅是向右下方倾斜的，即无差异曲线的斜率是负值，即随着商品1数量的连续增加，商品2必须不断减少，而且无差异曲线的斜率是递减的。无差异曲线的这一特点是由商品的边际替代率递减规律所决定。