回归分析方法是研究变量和变量之间依存关系的一种数学方法。根据回归分析涉及变量的多少，可以分为单元回归分析和多元回归分析。在回归分析中，自变量是随机变量，因变量是非随机变量，由给定的多组变量和因变量资料，研究各自变量和因变量之间的关系，形成回归方程。回归方程根据自变量和因变量之间的函数形式，又可分为线性回归方程和非线性回归方程两种。回归方程求得后，如给定各自变量数值，即可求出变量值。

回归分析中，又可依据描述自变量与因变量之间关系形态的回归函数是线性还是非线性，分为线性回归分析可以概括为

单元回归法是多元回归法的特例，对于非线性回归问题，通常应用变换把其化为线性回归问题。因此，在回归分析中，只要掌握线性回归方程的解法，非线性问题也就可以解决。

在负荷预测问题中，回归方程的因变量一般是电力系统的负荷，自变量是影响电力系统负荷的各种因素，如社会经济、人口、气候等。设它们之间的内在关系是线性的，回归方程为(www.daowen.com)

给定m组观察值（yi，xi1，xi2，…，xin）（i=1，2，…，m），代入式（12-21），有m个方程，写成矩阵形式为

式中

b为待求的n+1个回归系数。利用最小二乘法，使观察值y和估计值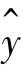^的残差平方和最小，可得正规方程，解正规方程可求出回归系数，从而确定回归方程，即可用来进行预测了。