不同的预测周期，B（t）分量具有不同的内涵。对于超短期负荷预测，B（t）近似线性变化，甚至是常数；对于短期负荷预测，B（t）一般呈周期性变化；而长期负荷预测中，B（t）呈明显增长趋势的周期性变化。

所以，对于基本正常负荷分量，可用线性变化模型和周期变化模型描述，或用二者的合成共同描述，即

式中　X（t）——为线性变化模型负荷分量；

　　　Z（t）——为周期变化模型负荷分量。

线性变化模型可以表示为

式中 a——线性方程的截距分量；

　　　b——线性方程的斜率。

1.线性变化模型

超短期负荷变化直接采用线性变化模型，将前面时刻的负荷描成一条直线，其延长线即可预测下一时刻的负荷，如图12-3所示。短期负荷日均值接近于常数，长期负荷年均值增长较大，甚至需要非线性模型描述。

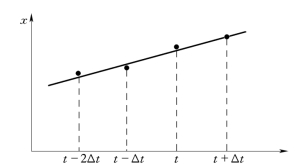
图12-3　负荷线性变化模型(www.daowen.com)

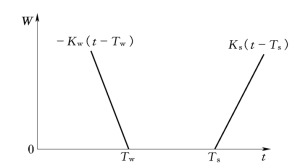
图12-4　天气敏感负荷模型

针对短期负荷预测，将历史上一段日负荷L按时序画在一张纸上，总体看来是一条斜率接近于零的直线，可用线性模型来描述。

2.周期变化模型

周期变化模型，是用来反映负荷按日、按月、按年的周期变化特性，其周期变化规律可以用日负荷系数Zi（t）表示为

式中　Li（t）——一天中各小时的负荷；

　　　Xi——当天的日负荷平均负荷。

将逐小时做出的日负荷变化系数的平均值，连接起来就是一天总的周期变化曲线。把这种反映一天24h负荷循环变化规律的模型称为日周期变化模型，即

式中　n——过去日负荷的天数；

　　　Zi（t）——过去第i天第t h负荷变化系数。

这样，按线性模型预测B（t）的负荷均值X（t），按周期变化模型预测B（t）的周期负荷系数Z（t），用式（12-2）就可得到基本负荷分量B（t）。