1.损失因数的定义

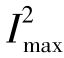损失因数是在线损理论计算中常用的系数之一。设损失因数为F，其值等于在计算时段内的平均功率损失ΔPav与最大负荷下功率损失ΔPmax之比，亦指在计算时段T内电流平方的平均值和最大电流的平方值之比，即

上式说明，可利用最大负荷下的功率损失ΔPmax计算时间T内的电能损耗，即

2.极端情况下的损失因数

如图11-1（a）、（b）分别表示了两种极端情况下的负荷曲线。

图11-1　极端情况下负荷曲线

图11-1（a），其负荷率f可近似表示为

因为图11-1（a）中最小电流Imin可近似认为其值等于0。

而损失因数为

由上式可看出F=f。

如设图11-1（b）最小负荷率为

则此时负荷率为(www.daowen.com)

因为最大负荷Imax所经历的时间t趋于0，且Iav=Imin。

损失因数为

对应图11-1（a），最小负荷Imin≈0，F=f；对应图11-1（b），最大负荷所经历时间，t≈0，F=f2。若将F定为纵坐标，f定为横坐标，与图11-1（a）相应的是直线；与图11-1（b），相应的为抛物线。如图11-2所示。一般情况下，负荷曲线介于图11-1（a）、（b）之间，因此，损失因数将介于直线和抛物线之间，如图11-2中的虚线所示。它们的关系可表示为

式中　β——与网络负荷曲线形状、网络结构、负荷特性有关的常数，通常β=0.1～0.4。

当β=1时，F=f；当β=0时，F=f2。一般，当负荷曲线接近于图11-1（a）时，β取较大值；而当负荷曲线接近于图11-1（b）时，β取较小值。

3.损失因数表达式

对于不同的配电网，β可取0.2或0.3，此时损失因数为

对于输电系统，Wolf提出用下式经验公式

在式（11-14）中，F仅由负荷率f决定，但f不能完全代表负荷曲线的形状，在相同的f值下，负荷曲线的最小负荷率α往往是不同的，所以损失因数F也将不同。

若近似认为负荷曲线按Bata概率分布而变化，就可以导出α与F的关系，经整理，得

图11-2　F与f的关系曲线