结构方程模型（Structural Equation Modeling，简称SEM）是一种通过研究显在变量和潜在变量，建立、估计、检验因果关系模型的验证性方法，也称为潜在变量模型（Latent Variable Models，简称LVM）。它是在20世纪60年代提出来的一种统计分析法，到了80年代逐渐成熟，在应用统计学上使用较多，是多元数据分析的重要工具。结构方程模型可以替代多重回归、通径分析、因子分析、协方差分析等方法，对某项指标与其他单项指标间的相互关系，以及对总体的影响作用给予分析并得出结果。结构方程模型结合了集成因素分析和路径分析这两种传统的统计方法，通过检验模型中的潜在变量（Latent Variables）、外显变量（Manifest Variables）及误差变量（Error Variable）之间的关系，并对变量间的路径关系进行研究进而评估结构模式的配适性。

结构方程模型主要研究两个内容：一个是通过研究外显变量和潜在变量之间的关系，从而得出测量模型；另一个是通过研究潜在变量之间的关系，从而得出潜在结构模型。

在构建测量模型时，假设X是外源观测变量指标，Y是内源观测变量指标，η是内源潜变量，ξ是经过标准化处理之后的外源潜变量，δ是X的测量误差，ε是Y的测量误差，λX是X与外源潜变量ζ之间的关系，λY是Y与内源潜变量η之间的关系。因此，测量模型的方程式为：

在构建潜在结构模型时，假设β是内源潜变量之间相互影响的路径系数，γ是外源潜变量对内源潜变量影响的路径系数。因此，潜在结构模型的方程式为：

下面举一个例子。假设有M个观测变量，对每个观测变量有N个观测值，可以将数据转换成N*M的矩阵，通过结构变量之间的关系可以得到如下结构方程组：

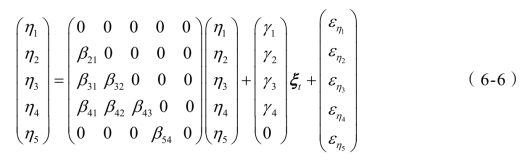
结构变量与观测变量之间的关系也可以用方程表示出来。设结构方程模型有k个结构自变量和m个结构因变量，与结构变量中的自变量ξt对应的观测变量为：

这里K（t）是与第t个结构自变量相联系的观测变量个数。假设观测变量k=1，而K（1）=5，则与结构变量中的因变量ηi对应的观测变量为：

这里L（i）为与第i个结构因变量相联系的观测变量个数。假设m=5，而L（i）=4，3，5，4，3，则从观测变量到结构变量的观测方程可以表达为：

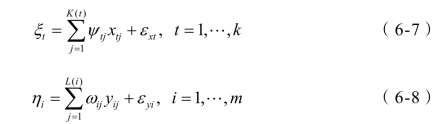
其中ψtj，ωij 是从观测变量到结构变量的汇总系数，εxt，εyi是随机误差项。

根据路径分析的思想，我们也可以认为观测变量的变化是来源于它所对应的结构变量，于是从结构变量到观测变量的观测方程组还可以表达为：

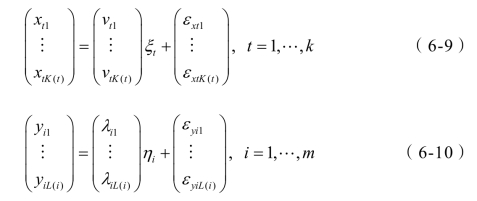
其中vtj，λij是从结构变量到观测变量的载荷系数，带下标的ε还是误差项。我们可以把方程组（6-6），（6-7），（6-8）称为带有正向观测的结构方程模型，而把方程组（6-6），（6-9），（6-10）称为带有逆向观测的结构方程模型。

在一般情形下，结构自变量不一定只有1个，结构因变量也不一定是5个，结构方程系数形式除了要求对角线是0外也可以不同于式（6-6）。下面采用向量与矩阵记法来描述结构方程模型。

记ξ′=，设η的系数矩阵为m阶方阵，记为B，ξ的系数矩阵为m×n阶矩阵，记为Γ，残差向量为，则结构方程组（6-6）可以一般表示为

记观测向量，再记系数，则方程组（6-11），（6-7），（6-8）合并为：(www.daowen.com)

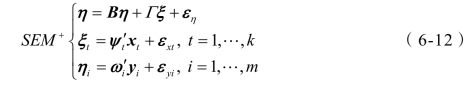
则称SEM+为带有正向观测的结构方程模型。

记，则观测方程组（6-9）可以表示为：

方程组（6-10）可以表示为：

方程组（6-11），（6-13），（6-14）合并为：

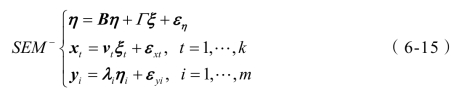
则称SEM-为带有逆向观测的结构方程模型（童乔凌等，2009）。

本研究使用AMOS 7.0对结构方程模型的参数进行估计和检验，并运用极大似然估计（Maximum Likelihood Estimate，简称MLE）对初始概念模型（见图6-2）的参数进行估计及检验。通过调整自由参数个数、对比卡方值的变化情况，依据各路径参数的显著性对模型进行修正，得出参数及数据拟合度相对较高的模型。

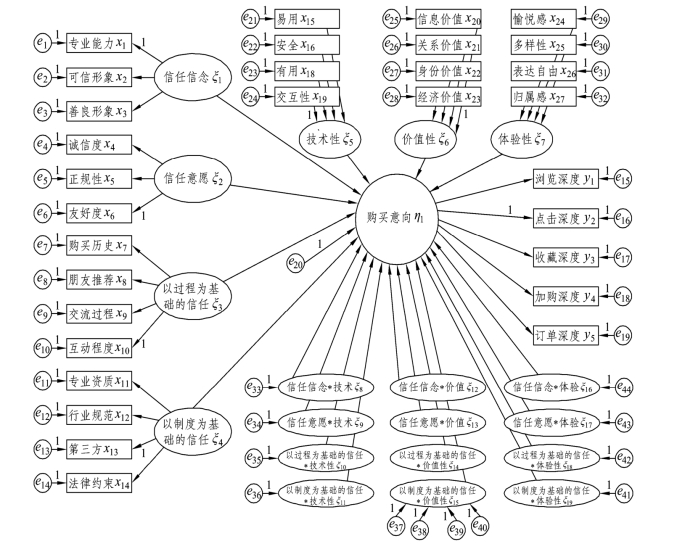
图6-2　初始概念模型

模型拟合度从拟合指数（绝对拟合指数、相对拟合指数、简约拟合指数）、拟合路径系数的显著性两方面进行评价。其中，绝对拟合指数从卡方自由度比、近似误差均方根、拟合优度、均方根误差、赋范拟合指数等方面对模型的拟合优度进行评价；相对拟合指数从增量拟合指数、塔克-刘易斯指数、比较拟合指数等方面对模型的拟合优度进行评价；简约拟合指数从简约拟合优度、简约比较拟合指数、调整拟合优度、简约赋范拟合指数等方面对模型的拟合优度进行评价。若路径系数＞5%，表明未通过显著性检验，可通过拟合指数进行修正，即通过专业知识和实际情况，扩展或限制初始模型，以使拟合优度变高。陈思敏等（2018）在研究中指出，当模型具有较强现实意义的时候，拟合优度作为参考指标并非越高越好。

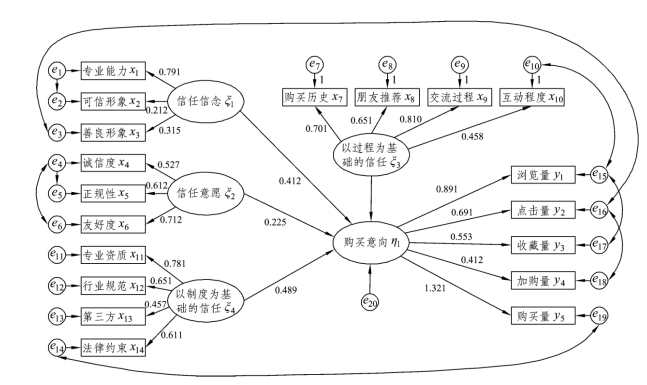
图6-3　修正后的基本模型

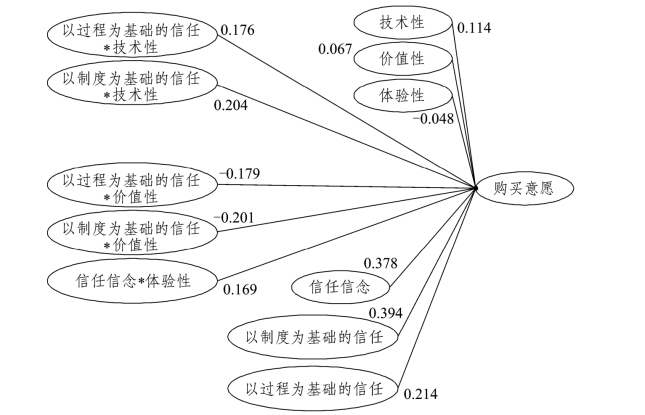
图6-4　修正后的结构模型

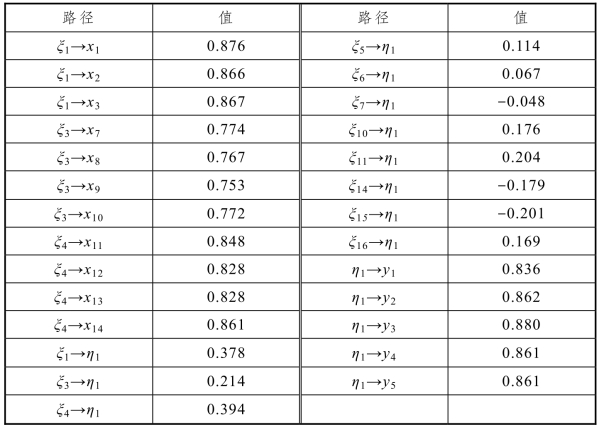
经过修正，形成拟合效果较好的模型（见图6-3和图6-4），通过表6-14和表6-15可以看出，修正模型与数据集拟合较好，从而证明了初始概念模型（见图6-2）的合理性及有效性。

表6-14　模型拟合指数

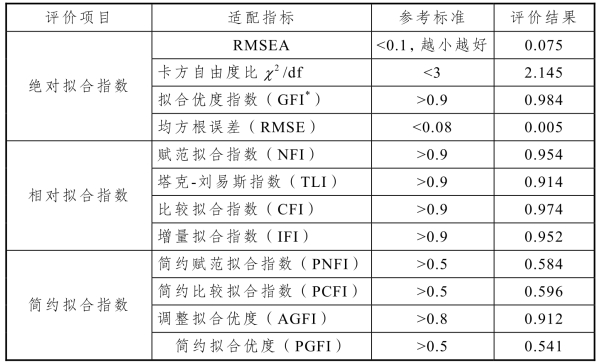
表6-15　修正模型标准化路径系数