常用的异方差检验方式有以下三种：White检验、Glejser检验和自回归条件异方差（ARCH）检验。

1.White检验

H.White在1980年提出White检验，这是一种不需要对数据进行排序的回归检验方法。具体计算方法如下：

（1）首先对上式进行OLS回归，求出残差uˆt。

（2）做如下辅助回归式：

即对原回归式中的各解释变量、解释变量的平方项、交叉积项进行OLS回归，上述公式中的常数项需要保留。计算辅助回归式（5-2）的可决系数R2。

White检验的步骤如下：

第一步：White检验的零假设和备择假设是：

H0：式（5-1）中的ut不存在异方差；

H1：式（5-1）中的ut存在异方差。

第二步：在不存在异方差假设条件下，其统计量为

其中T表示样本容量，R2是辅助回归式（5-2）的OLS估计式的可决系数。自由度5表示辅助回归式（5-2）中解释变量项数（不计算常数项）。TR2属于LM统计量。

第三步：判别规则是：

若TR2≤，接受H0（ut具有同方差）；

若TR2＞，拒绝H0（ut具有异方差）。

2.Glejser检验(www.daowen.com)

若与解释变量xt之间存在函数关系，则表明存在异方差。通常检验形式如下：

Glejser检验的特点是：

（1）可检验递增型异方差和递减型异方差。

（2）当发现有异方差时，异方差的具体表现形式也就被发现了。

（3）计算量比较大。

（4）在原模型含有多个解释变量值时，可把拟合成多变量回归形式。

3.自回归条件异方差（ARCH）检验

自回归条件异方差检验中先将看作误差滞后项，…的函数，然后进行误差项二阶矩的自回归计算。

首先，将辅助回归式定义为

其次，将LM统计量定义为

其中R2是辅助回归式（5-4）的可决系数。

当H0：α1=…=αn=0时，ARCH渐近服从分布。

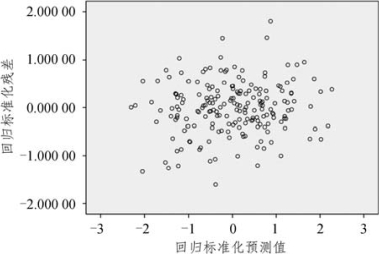
图5-1　残差散点图

图5-1是计算得到的回归残差散点图。从图5-1可以看出，残差散点的分布不具备规律性，比较分散，这说明根据回归模型计算得到的方差是相同的，解释变量之间不存在异方差问题。