1.概念

直方图（histogram）法是从总体中随机抽取样本，将从样本中获得的数据进行整理，从而找出数据变化的规律，以便测量工序质量的好坏。直方图是常用的质量检验（QC）工具。

2.作图步骤

第一步 收集数据。数据个数一般为50个以上，最少不少于30个。

第二步 求极差R。在原始数据中找出最大值和最小值，计算二者的差就是极差，即R=Xmax-Xmin。

第三步 确定分组的组数和组距。一批数据究竟分多少组，通常根据数据个数的多少来定。可参考表13-4：

表11-5　直方图分组数表

第四步 确定各组界限。 先取测量值单位的1/2。分组界应该能够包括最大值和最小值。第一组的上下限值为最小值+/-（h/2）。第一组的上界限值就是第二组的下界限值，第二组的下界限值加上组距就是第二组的上界限值，也就是第三组的下界限值，依次类推，可定出各组的组界。为了计算的需要，往往要决定各组的中心值。每组的上下界限相加除以2，所得数据即为组中值。组中值为各组数据的代表值。

第五步 制作频数分布表。将测得的原始数据分别归入到相应的组中，统计各组的数据个数，即频数fi， 各组频数填好以后检查一下总数是否与数据总数相符，避免重复或遗漏。

第六步、画直方图。以横坐标表示质量特性（如上表中的中心值），纵坐标为频数，在横轴上标明各组组界，以组距为底，频数为高，画出一系列的直方柱，就成了直方图。(www.daowen.com)

第七步 在直方图的空白区域，记上有关的数据的资料。如样本数，平均值，标准差等。

3.常见类型（如图11-8所示）

（1）标准型（对称型）。数据的平均值与最大和最小值的中间值相同或接近，平均值附近的数据频数最多， 频数在中间值向两边缓慢下降，并且以平均值左右对称。这种形状是最常见的。

（2）锯齿型。做频数分布表时，如分组过多，会出现此种形状。另外，当测量方法有问题或读错测量数据时，也会出现这种形状。

（3）偏态型。数据的平均值位于中间值的左侧（或右侧），从左至右（或从右至左），数据分布的频数增加后突然减少，形状不对称。

（4）平顶型。当几种平均值不同的分布混在一起，或某种要素缓慢变化时，常出现这种形状。

（5）双峰型。靠近直方图中间值的频数较少，两侧各有一个“峰”。当有两种不同的平均值相差大的分布混在一起时，常出现这种形状。

（6）孤岛型。在标准型的直方图的一侧有一个“小岛”。出现这种情况是夹杂了其他分布的少量数据，如工序异常、测量错误或混有另一分布的少量数据。

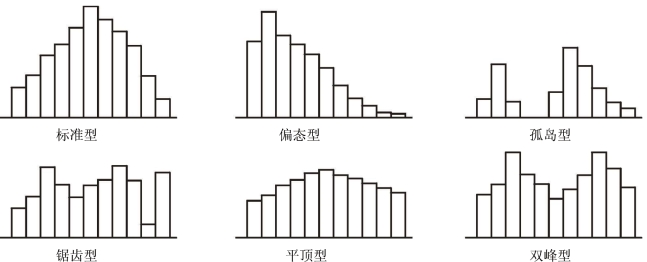
图11-8　不同形状的直方图