一、描述统计方法

描述性统计是通过对质检得到的数据进行归纳分析从而反映产品各种质量特征的一种分析方法。在描述性统计中，主要使用集中趋势、离散程度的分布形态描述数据的集中性、分散性，归纳出产品的质量状况。其中，集中趋势用来反映数据的代表水平，常用的指标有平均值、中位数和众数等；离散程度主要是用来描述数据之间的差异程度，反映了数据偏离中心的分布情况，常用的指标有方差和标准差等。

1.数据的集中趋势分析

（1）平均值：描述的是所抽取样本质检数据的平均值，是用一组数据中所有数据之和除以这组数据的个数所得的结果。平均值是表示一组数据集中趋势的量数，反映数据集中趋势的一项指标。用平均数表示质量数据趋势，具有直观，简洁的特点。例如，在产品质量抽样调查中，可以利用样本的平均值判断某批次产品的质量。

对于某批次产品质量抽检数据集合为｛x1，x2，…，xn｝，其平均值x—的计算公式为

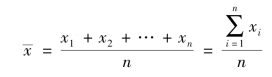
（2）中位数：描述的是一组数据的典型情况，是按顺序排列在一起的一组数据中居于中间位置的数，又名中数。当数据数量为奇数时，中位数应该是在对一组数进行排序后，处于正中间的一个数；当数据数量为偶数时，中位数则应是中间两个数的平均数。因此，中位数可能是数据中的某一个，也可能根本不是原有的数。

例如，对于某批次产品质量抽检数据集合按顺序从小到大排列为｛x1，x2，…，xn｝，当n为奇数时，中位数m0.5的计算公式为

当n为偶数时，中位数m0.5的计算公式为

（3）众数：指在统计分布上具有明显集中趋势点的数值，代表数据的一般水平。也是一组数据中出现次数最多的数值，有时众数在一组数中有好几个。

2.数据的离散程度分析

（1）极差：极差为数据样本中的最大值与最小值的差值。它反映了数据样本的数值范围，是最基本的衡量数据离散程度的方式，受极值影响较大。极差的计算公式为

（2）方差：方差用来反映一组数据的变异程度。方差的计算公式为

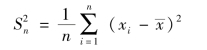
（3）标准差：标准差是每一个变量（观察值）与总体均数之间的差异，是方差的算数平方根。标准差的公式为

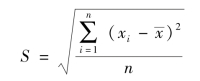
简单来说，标准差是一组数据平均值分散程度的一种度量。一个较大的标准差，代表大部分数值和其平均值之间差异较大；一个较小的标准差，代表这些数值较接近平均值。例如，A、B两组各有3件螺母样品，A组螺母的直径分别为70 mm、74 mm、78 mm，B组螺母的直径分别为73 mm、74 mm、75 mm。这两组的平均值都是74 mm，但A组的标准差为3.27 mm，B组的标准差为0.82 mm，说明A组螺母直径之间的差距比B组大得多。

质量数据的图形统计分析方法

二、图形统计方法

在质量数据分析中，采用图形化的方式可以直观地分析数据，找出问题的原因。目前比较常见的图形统计方法包括直方图法、分层法、排列图法、控制图法、矩阵图法、矢线图法和关系图法等。下面重点介绍其中几个简单的方法。

1.直方图法

（1）直方图法的作用。直方图法是由一系列高度不等的纵向条纹或线段表示质量数据特性分布的情况，一般用横轴表示数据类型，纵轴表示分布情况。通过观察直观图的形状，可以判断生产过程是否稳定，并预测生产过程的质量。直方图法适用于对大量质量数据的分析，根据数据找出质量规律，了解产品质量的分布情况和特征数量，一般对总体的质量情况进行分析。

直方图的作用主要包括以下三个方面：

显示质量波动的状态；较直观地传递有关过程质量状况的信息；在研究质量波动状况之后，就能掌握过程的状况，从而确定在什么地方集中力量进行质量改进工作。

图5－56所示为一个金属制品拉伸强度质量数据的直方图示例。其中，横坐标表示质量特性即拉伸的强度；纵坐标表示频数即符合该拉伸强度的制品个数；虚线为所有样本拉伸强度数据的均值。

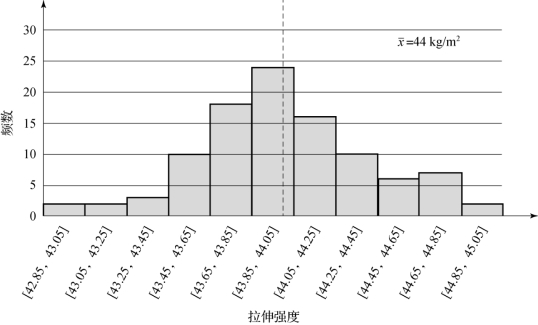
图5-56　直方图示例

（2）直方图的绘制。将收集到的质检数据划分为若干相等的区间，将各区间内质检数据数值出现的频数用柱状排列，具体步骤如下：

①收集数据，求出其最大值和最小值。数据的数量应在100个以上，在数量不多的情况下，至少也应在50个以上。

②将数据分成若干组，并做好记号。一般分组数量需要根据样本数据容量来确定，组数的取值可以参考表5－5。

表5-5　样本容量与组数的对应参考值

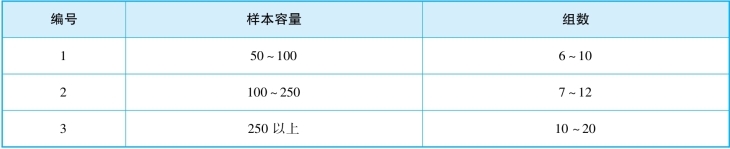
③计算组距的宽度。用最大值和最小值之差去除组数，求出组距的宽度。

④计算各组的界限位。各组的界限位可以从第一组开始依次计算，第一组的下界为最小值减去最小测定单位的一半，第一组的上界为其下界值加上组距。第二组的下界限位为第一组的上界限值，第二组的下界限值加上组距，就是第二组的上界限位，依此类推。

⑤统计各组数据出现频数，作频数分布表。

⑥作直方图。以组距为底长，以频数为高，画出一系列的直方图。

（3）直方图的示例应用。

某工厂生产了一批金属制品，共5 000个，质检部采取抽检的方式对该批次产品进行质量检查，每天抽取10个，共10天对金属制品的拉伸强度进行检测，获取数据100个，质检数据如表5－6所示。

表5-6　金属制品拉伸强度的样本数据（单位kg／cm2）

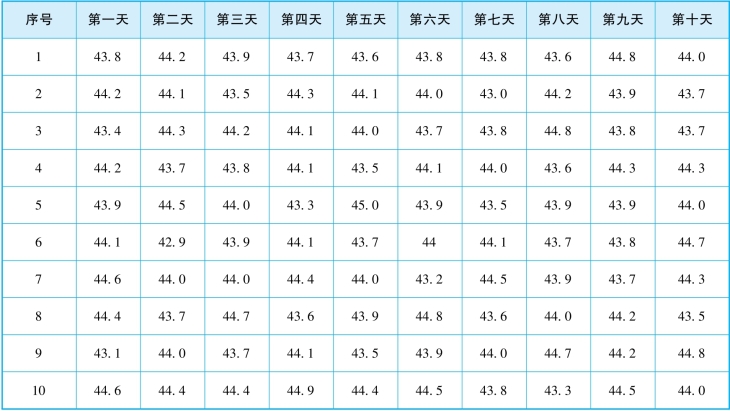
经过计算，频数分布如表5－7所示。

表5-7　频数分布表

绘制直方图，直方图效果如图5－57所示。

图5-57　用直方图法分析拉伸强度

（4）直方图的形状分析。

通过对直方图的形状分析，可以了解质检特性是否正常，常见的直方图形状及其特性分析如表5－8所示。

表5-8　直方图的形状分析

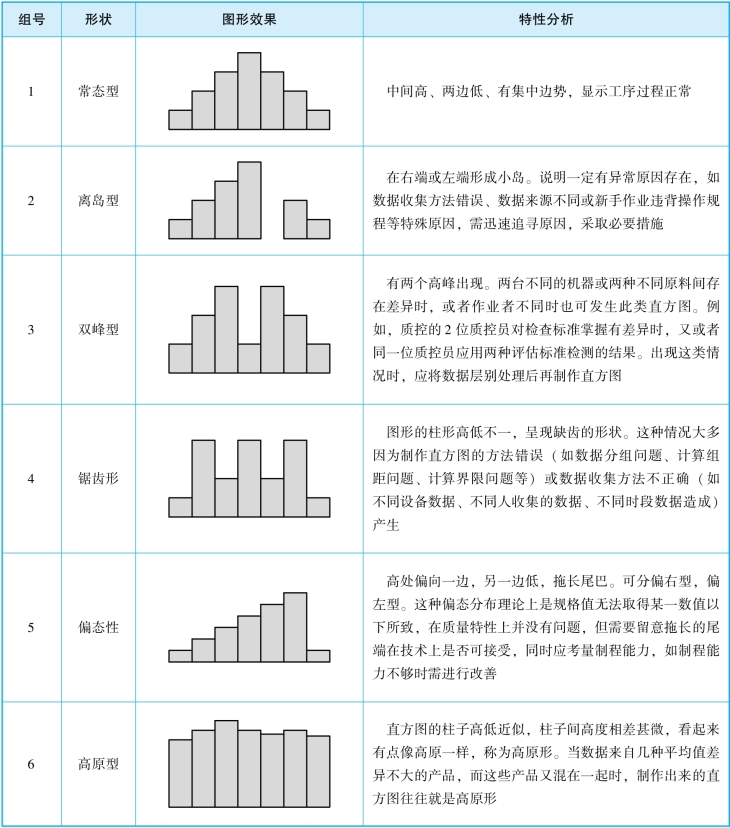(www.daowen.com)

2.分层法

（1）分层法的作用。分层法又叫分类法、分组法。它是按照一定的标志，将收集到的大量有关某一特定主题的统计数据加以归类、整理和汇总的一种方法。分层的原则是使同一层次内的数据波动幅度尽可能小，而层与层之间的差别尽可能大，这样可以使数据反映的事实更加明显、更集中，从而找准问题，对症下药。

常用的分层标志如下。

按人员类型分层：可按产地、批号、制造厂、规格、成分等分层。

按设备类型分层：可按设备类型、新旧程度、不同的生产线、工夹具类型分层。

按材料类型分层：可按产地、批号、制造厂、规格、成分等分层。

按方法类型分层：可按不同的工艺要求、操作参数、操作方法、生产速度分层。

按测量类型分层：可按测量设备、测量方法、测量人员、测量取样方法、环境条件等分层。

按时间类型分层：可按不同的班次、日期等分层。

按环境类型分层：可按照明度、清洁度、温度、湿度等分层。

按其他条件分层：可按地区、使用条件、缺陷部位、缺陷内容等分层。

分层的一般步骤如下：

①收集数据。

②将采集到的数据根据不同的目的选择分层标志。

③分层。

④按层归类。

⑤画分层归类图。

（2）分层法的示例应用。

在对某一批缸体缸盖连接情况的调查分析中，共检查了50个发动机缸体，其中不合格19个，不合格率为38%。其存在严重的质量问题，试用分层法分析质量问题的原因。

现已查明这批缸体生产是由A、B、C三个师傅操作的，而气缸垫是由甲、乙两个制造厂家提供的，因此，分别按操作者和气缸垫制造厂家进行分层分析，即考虑一种因素单独的影响，如表5－9和表5－10所示。

表5-9　按操作者分层

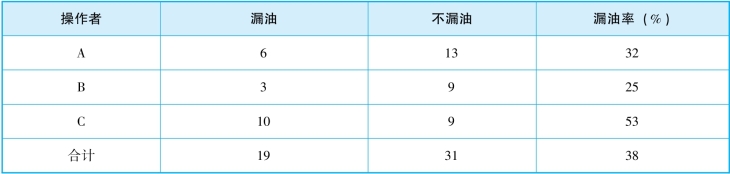
表5-10　按制造厂家分层

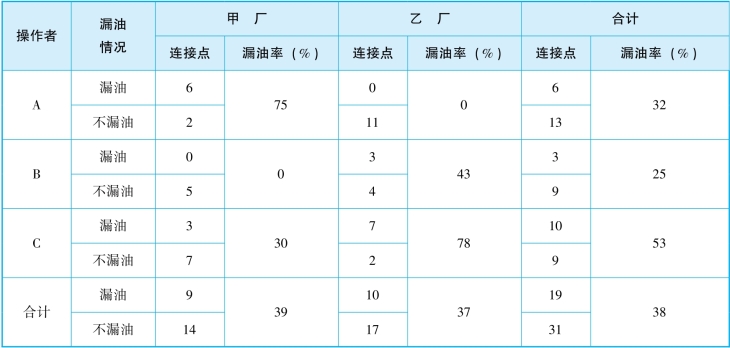
通过表5－9和表5－10分层分析可以看出，在操作者层面上，操作者B师傅的质量较好，漏油率为25%；在制造厂家层面上，甲厂和乙厂所提供的气缸垫，漏油率都较高且相差不大。为了找出问题所在，再进一步采用综合分层进行分析，考虑两种因素交叉影响的结果，如表5－11所示。从对表5－11的综合分层法的分析可知，在使用甲厂提供的气缸垫时，应采用操作者B师傅的操作方法比较好；在使用乙厂提供的气缸垫时，应采用操作者A师傅的操作方法比较好，这样能够提高缸体缸盖连接的质量。

表5-11　两种因素综合分层分析连接问题

3.排列图法

（1）排列图法的作用。排列图法就是将影响质量的各种因素，按照出现的频数从大到小的顺序排列在横坐标上，在纵坐标上标出因素出现的累积频数，并画出对应的变化曲线的分析方法。其作用包括两个方面：一是按主要顺序显示出每个质量改进项目对整个质量问题的影响；二是识别进行质量改进的机会。

排列图由两个纵坐标、一个横坐标、若干个直方图形和一条曲线组成。其中左边的纵坐标表示频数，右边的纵坐标表示频率，横坐标表示影响质量的各种因素。

如图5－58所示，若干个直方图形分别表示质量影响因素的项目，直方图形的高度则表示影响因素的大小程度，按大小顺序由左向右排列，曲线表示各影响因素大小的累计百分数。这条曲线称为帕累托曲线。实际应用中，通常按帕累托曲线划分主次因素，其中0～80%为A类问题，即主要因素，要重点管理；80%～90%为B类问题，即次要问题，要次重点管理；90%～100%为C类问题，即一般问题，要适当加强管理。

（2）排列图的绘制。

选择要进行质量分析的项目；

选择用来进行质量分析的度量单位，如出现的次数（频数、件数）、成本、金额或其他；

选择进行质量分析的数据的时间间隔；

画横坐标；

画纵坐标；

在每个项目上画长方形，它的高度表示该项目度量单位的量值，显示出每个项目的影响大小；

图5-58　排列图

由左到右累加每个项目的量值（以%表示），并画出累计频率曲线（帕累托曲线），用来表示各个项目的累计影响；

利用排列图确定对质量改进最为重要的项目（关键的少数项目）。

（3）排列图法的示例应用。

某公司一周内对某一批次缸体产品进行多次检验，发现的不良记录如表5－12所示，根据统计的记录，运用排列图进行分析。

表5-12　一周内产品不良记录

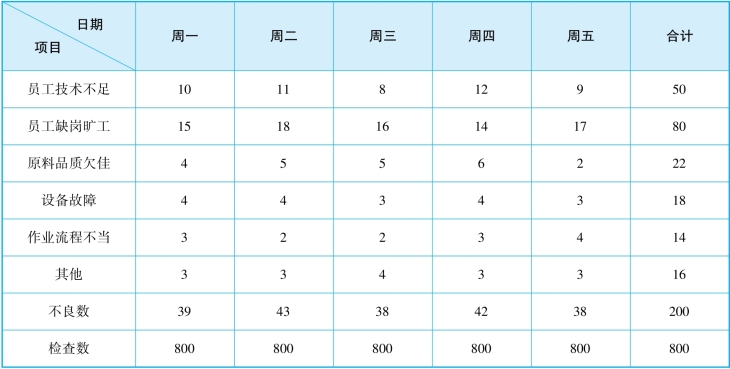
按发生次数的顺序（由大致小，有其他项者无论是否为最小，一律放置于最后）将项目及次数计入不良分析统计表中，如表5－13所示。

表5-13　不良分析统计表

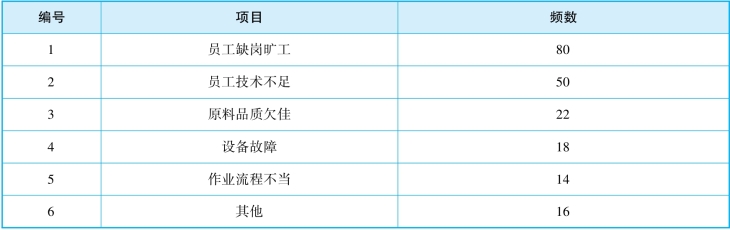
对统计表中的不良数进行计算，获取各个项目的不良数量、累计数量、频率及累计频率，如表5－14所示。

表5-14　不良分析换算统计表

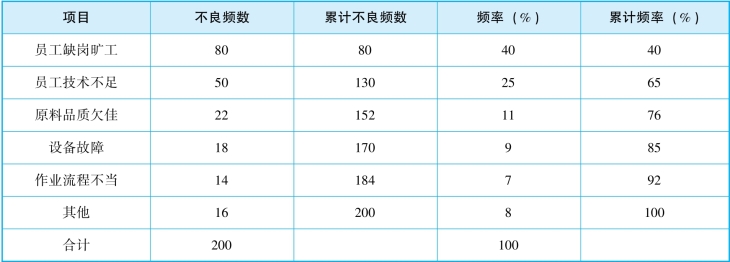
建立坐标轴，以左纵轴表示不良数，右纵轴表示百分比，横坐标轴表示不良项目，根据不良数绘制柱形图，根据累计频率绘制帕累托曲线，最终绘制成排列图，具体如图5－59所示。

根据排列图，将累计频率按照0～80%、80%～90和90%～100%分为三个部分，各曲线下面所对应的影响因素分别为A、B、C三类因素。本例中A类即主要原因是员工缺岗旷工、员工技术不足和原料品质欠佳，B类即次要原因是设备故障，C类即一般原因是作业流程不当和其他等。因此后面改进的重点应主要放在A类问题上。