已知假设ed2＝α1ed1，α1为制造商M2线上渠道促销努力的变化率，意味着相对于制造商M1的线上市场渠道促销努力，制造商M2线上渠道促销努力的变化程度。可以得到如下启示：

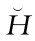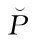
第一，观察图6－17、6－18，根据πr≥0得出0≤α1≤86.111，在此范围内π2≥0，π1≥0。故得出取值范围为0≤α1≤86.111。 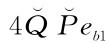＝－51.804＜0， ＝－206.43＜0，＝－20.66＜0， －＝5 570.52＞0。进一步观察图6－19，在0≤α1≤86.111范围内，er≥0恒成立。并且可以求出，er≥0的取值范围为0≤α1≤293. 592。

图6－17 线上渠道促销努力变化率α1下的零售商r收益变化规律

第二，进一步观察图6－17、6－18、6－19，在0≤α1≤86.111范围内，随着参数α1逐渐增大，线下市场快速缩水，本来就生存维艰的线下零售商r处境更加恶化，面临着倒闭以退出市场竞争的危险。而随着弱势线上制造商M2在线上市场的渠道促销力度越来越大，其地位上的劣势明显得以改善，而收益上升最为显著，说明相对于强势制造商M1，提升线上市场的渠道促销力度能够大大增强线上制造商M2的线上市场竞争能力。然而，强势制造商M1一方面面临线下市场份额的快速缩水，另一方面其线上市场份额又被弱势线上制造商M2侵占，导致其收益曲线呈现出单调递减的特点。直至α1＝86.111，此时π1＝5 020.86，π2＝19 815.7，πr＝0，er＝0.39。对于强势制造商M1来说，要想保证其本身的渠道主导地位不变并且获得最大收益，参数α1应该越小越好。如果要满足π1≥π2的收益前提，合理的参数取值区间为0≤α1≤6.419。

图6－18 线上渠道促销努力变化率α1下的供应链成员收益变化规律

图6－19 线上渠道促销努力变化率α1下的零售商r努力水平变化规律

第三，观察图6－20、6－21，在0≤α1≤86.111范围内，随着参数α1逐渐增大，曲线p2分别超越了曲线p1与曲线pr，交点分别为（6.057，18.445）及（9.378，18 .724）。这意味着弱势线上制造商M2在线上市场的渠道促销力度越来越大，必然会带来其线上市场销售价格的递增，以满足促销带来的高成本支出。然而，其他各类价格曲线均呈现出递减趋势。其中，随着弱势线上制造商M2在线上市场的渠道促销力度逐步增大，曲线pr始终处于曲线w上方，保证了线下零售商r能够获得正向收益，然两条曲线在递减过程中呈逐步靠拢的趋势。当α1＝0时（pr－w ）＝1.246，当α1＝86.111时，（pr－w）＝0.88，说明线下零售商r的收益逐步减少，且曲线p1的递减速度低于曲线pr，故双方在α1＝65.514处相交，弱势线上制造商M2的渠道促销努力对线下零售商r的影响高于强势制造商M1，直至α1＝86.111。此时，相关最优变量结果为p2＝25.167，pr＝16.353，w＝15.472，p1＝16.485。(www.daowen.com)

图6－20 线上渠道促销努力变化率α1下的供应链成员定价变化规律（α1∈（0，86.111））

第四，观察图6－22、6－23，在0≤α1≤86.111范围内，随着参数α1逐渐增大，弱势线上制造商M2在线上市场的渠道促销力度越来越大，强势制造商M1的总需求曲线单调递减，线上制造商M2的总需求曲线单调递增。结合前面图6－20、6－21观察可得，参数α1的增大能促使弱势线上制造商M2的销售价格上升而需求曲线递增，故弱势线上制造商M2必然会加大线上市场的渠道促销力度来提升收益。当α1＝5. 03时，弱势线上制造商M2的需求曲线超过了强势制造商M1的需求曲线。当α1＝86.111时，D2＝1 184.54，D1＋Dr＝580.753。对强势制造商M1来说，为保证其产能总量的第一地位，参数α1应该越小越好，相对于弱势线上制造商M2，至少应该保证0≤α1≤5.03。

图6－21 线上渠道促销努力变化率α1下的供应链成员定价变化规律（α1∈（0，20））

图6－22 线上渠道促销努力变化率α1下的制造商M1与M2需求量变化规律（α1∈（0，86.111））

图6－23 线上渠道促销努力变化率α1下的制造商M1与M2需求量变化规律（α1∈（0，20））