强势制造商M1、弱势线上制造商M2及零售商r在线上线下市场的促销活动会影响到消费者对线上线下两类市场认可程度的改变,进而影响到线上线下市场份额的划分,这种情形在弱势线上制造商M2的竞争地位上升,即由最弱势升为竞争的次主导地位时,变得更为显著。不同市场的顾客需求量不仅与展开博弈的三方供应链成员企业的定价机制有关,更与三方企业的促销努力程度密切相关。强势制造商M1、弱势制造商M2及零售商r的需求函数仍保持不变,为
D1(p1,w,ed1,eb1)=[ae-mp1+np2+θ(pr-p1)+γed1-λed2-φ(er-ed1)]eb1
D2(p2,ed2,eb2)=[ae-mp2+np1+θ(pr-p2)+γed2-λed1-φ(er-ed2)]eb2
Dr(pr,er)=ar-mpr+θ(p1-pr)+θ(p2-pr)+γer+φ(er-ed1)+φ(er-ed2)
模型四的基本模型如下图5-10所示,较之于图3-1考虑进了线上线下市场促销因素的影响。
5.3.1 零售商r的利润函数
根据前文可知,零售商r的需求函数仍为
Dr(pr,er)=ar-mpr+θ(p1-pr)+θ(p2-pr)+γer+φ(er-ed1)+φ(er-ed2)
收益函数为
πr(pr,er)=(pr-w-cr)Dr(pr,er)-f(er)-F=(pr-w)[ar-mpr+θ(p1-pr)+θ(p2-pr)
对其进行一阶函数求导,有
可以得出,
2η(m+2)θ>(γ+2)φ2时,零售商r存在最大收益。
图5-10 模型四:线上制造商M2次主导下的基本模型(考虑促销因素)
根据一阶条件为零,可以得到 =(m+2θ)( pr- w),联立方程有
=(m+2θ)( pr- w),联立方程有
进一步化简得到
继续代入化简得到
令 ,则上面方程变为
,则上面方程变为
ar-φ(ed1+ed2)+θ(p1+p2)+ +
+ =0,故可以求得
=0,故可以求得
进一步地,收益函数
化简得到
令 =(m+2θ)-
=(m+2θ)-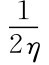 (γ+2φ)2=-
(γ+2φ)2=- ,则
,则
并得到如下定理:
定理5.5 线上线下市场并存下且考虑促销因素时,若线上制造商M2处于次主导地位,线下零售商r必定存在最优定价决策的条件为 <0。此时,线下零售商r的最优收益值为正值,即此时线下零售商r才有动力参与线上线下市场竞争。
<0。此时,线下零售商r的最优收益值为正值,即此时线下零售商r才有动力参与线上线下市场竞争。
推理5.2 线上线下市场并存下且考虑促销因素时,若线上制造商M2处于次主导地位,线下零售商r的渠道促销努力水平越高,其最优收益也越大。
推理5.3 线上线下市场并存下且考虑促销因素时,若线上制造商M2处于次主导地位,线下零售商r的购销差价越大,渠道促销努力水平越高。
推理5.4 线上线下市场并存下且考虑促销因素时,若线上制造商M2处于次主导地位,线上线下市场间的促销努力水平差异越大,顾客需求对渠道促销努力水平的反应越大,线下零售商r的最优收益越低。
5.3.2 制造商M2的收益函数
制造商M2的需求函数为
D2(p2,ed2,eb2)=[ae-mp2+np1+θ(pr-p2)+γed2-λed1-φ(er-ed2)]eb2
其收益函数为
π2=(p2-c2)D2(p2,ed2,eb2)-f(ed2)-f(eb2)
 =[ae-mp2+np1+θ(pr-p2)+γed2-λed1-φ(er-ed2)]eb2-(p2-c2)eb2(m+θ)
=[ae-mp2+np1+θ(pr-p2)+γed2-λed1-φ(er-ed2)]eb2-(p2-c2)eb2(m+θ)
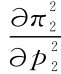 =-2(m+θ)eb2<0
=-2(m+θ)eb2<0
当(p2-c2)[ae-m p2+n p1+θ(pr-p2)+γed2-λed1-φ(er-ed2)]>κ时,函数π2(p2,ed2,eb2)随eb2单调递增,反之单调递减。
当 时,函数π2 (p2,ed2,eb)2 随ed2单调递增,反之单调递减。
时,函数π2 (p2,ed2,eb)2 随ed2单调递增,反之单调递减。
进一步得到,D*2(p2,ed2,eb) =(p2-c2)2eb2(m+θ)。根据一阶条件为零,有
[ae-mp2+np1+θ(pr-p2)+γed2-λed1-φ(er-ed2)]eb2-(p2-c2)eb2(m+θ)=0
进一步化简得到(https://www.daowen.com)
继续化简,得到
即
令
则有[2(m+θ)-θ ]p2=
]p2= +
+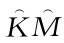 +(n+
+(n+ )p1[+
)p1[+ +
+ (γ+2φ)]w,求得
(γ+2φ)]w,求得
再令
则
并可以得到如下定理:
定理5.6 线上线下市场并存下且考虑促销因素时,若线上制造商M2处于次主导地位,线上制造商M2能够实现收益最优化。
推理5.5 线上线下市场并存下且考虑促销因素时,若线上制造商M2处于次主导地位,当 时,线上制造商M2的收益与渠道促销努力水平正相关,反之则为反相关关系;当
时,线上制造商M2的收益与渠道促销努力水平正相关,反之则为反相关关系;当 时,线上制造商M2的收益与品牌促销努力水平正相关,反之则为反相关关系。
时,线上制造商M2的收益与品牌促销努力水平正相关,反之则为反相关关系。
推理5.6 线上线下市场并存下且考虑促销因素时,若线上制造商M2处于次主导地位,当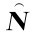 ≥0时,p*2与p*1正相关,反之则为反相关关系;当
≥0时,p*2与p*1正相关,反之则为反相关关系;当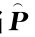 ≥0时,p*2与w正相关,反之则为反相关关系。
≥0时,p*2与w正相关,反之则为反相关关系。
推理5.7 线上线下市场并存下且考虑促销因素时,若线上制造商M2处于次主导地位,线上制造商M2的品牌促销努力水平与各项最优决策变量无关,与线上制造商M2的最优收益有关。
5.3.3 制造商M1的收益函数
根据前文所得有
又制造商M1的收益函数为
π1(p1,w,ed1,eb1)=(p1-c1)D1(p1,w,ed1,eb1)+(w-c1)Dr(pr,er)-f(ed1)-f(eb1)
首先针对变量p1进行寻优求导,得到
<0为函数存在最优收益的必要条件之一。
然后,对变量w进行寻优求导,得到
又有
当 >0时,函数单调递增,反之函数单调递减。
>0时,函数单调递增,反之函数单调递减。
当 >0时,函数单调递增,反之函数单调递减。
>0时,函数单调递增,反之函数单调递减。
此处令
则极值存在的条件为
进一步地,根据一阶条件为零,联立方程有
且最优收益函数为
鉴于方程的复杂性,这里不进一步求得最优变量p*1、w*的解析解。进而就可以求出其他最优解,如下表5-2所示。
表5-2 模型四的最优变量结果
续 表
并得到如下定理:
定理5.7 线上线下市场并存下且考虑促销因素时,若线上制造商M2处于次主导地位,制造商M1存在最优决策的条件为
推理5.8 线上线下市场并存下且考虑促销因素时,若线上制造商M2处于次主导地位,当批发价格高于生产成本时,制造商M1才会参与线上线下市场促销努力竞争。
5.3.4 供应链协调的实现条件
与5.2.5类似,此处不再赘述。
观察表5-2,可以得到如下几项结论:
第一,品牌促销努力水平不影响各项最优变量,但会影响到制造商M1与M2的最优收益。
第二, 作为判断条件,仅与强势制造商M1的品牌促销水平有关,与其他促销努力水平均无关系。
作为判断条件,仅与强势制造商M1的品牌促销水平有关,与其他促销努力水平均无关系。
第三,由于线下零售商r没有考虑到单位产品的店面租金等问题,故导致线下零售商r在较低价格情形下也会进行销售,实际上如果考虑进租金问题,零售商r的生存空间就微乎其微了。这种状态下,如果需要扶持和鼓励零售商r来维持线下市场的话,强势制造商M1就应该采取对应措施,供应链协调问题也可以进一步展开分析。零售商r需要增加店面租金和员工费用等固定成本F。
第四,供应链协调不存在。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







