为了探讨线上线下市场互融对供应链产能竞争优化及风险防范决策的影响，本节对参数假设赋值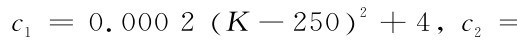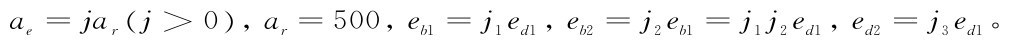， 其中，参数j为线上市场容量变化率，意味着相对于线下市场容量，线上市场容量所占比例，其反映了行业电子商务的发展程度。参数j越大，行业电子商务发展程度越高；参数j1为制造商M1品牌促销努力的变化率，意味着相对于制造商M1的线上市场渠道促销努力，其品牌促销努力的变化程度；参数j2为制造商M2品牌促销努力的变化率，意味着相对于制造商M1的线上市场品牌促销努力，线上制造商M2品牌促销努力的变化程度；参数j3为制造商M2线上渠道促销努力的变化率，意味着相对于制造商M1的线上市场渠道促销努力，制造商M2线上渠道促销努力的变化程度。

7.1.1 线上市场促销努力水平的影响

首先，观察图7－1可以发现，随着制造商M2线上渠道促销努力变化率j3的增加，制造商M1的最优产能呈极缓慢的下降趋势，说明提高制造商M2的线上市场渠道促销水平会降低制造商M1的最优产能，然降低速度很慢，影响效果极为有限。进一步观察附录7－1，发现参数j3的增加使得制造商M1与M2的生产成本均有下降，而制造商M1的产能分配比例保持略偏向线上市场的趋势，从0.788增加至0.793。相对于线下市场，制造商M1的产能分配比例也保持略偏向线上市场的趋势，从2.026增加至2.048。并且，参数j3的增加使得制造商M2需求量与收益均上升，线上售价同步上升。而制造商M1则采取降低批发价的策略来提高线下市场需求量并减缓线上市场的竞争压力，同时降低线上市场售价来保持线上市场需求量的适当上升，而总收益略有下降。零售商r则得益于批发价的下降而略微调低了零售价格，实现其总收益下降速度的减缓。

图7－1 线上促销努力变化率下的制造商M1最优产能决策

其次，进一步观察图7－1与附录7－1、7－2，发现在制造商M1线上品牌促销努力变化率j1的攻势下最优产能决策明显上升，两制造商的生产成本均上升。制造商M1的产能分配比例明显偏向线上市场，从0.146增加至1.233。而相对于线下市场，线上市场的产能分配比例也明显增大，从0.488增加至3.122。制造商M1线上品牌促销努力对制造商M2呈现出明显的“搭便车效应”，伴随其线上售价的上涨，需求量与总收益也明显上涨。制造商M1借助加大线上市场的品牌促销努力，提升了线下市场的批发价，将线下需求量转移至线上市场，使得两制造商的线上需求量明显提升。零售商r则采取提高零售价、降低服务水平等应对策略，来减缓线下零售收益的下降趋势。

第三，根据前文假设需满足条件p1＞w，pr＞p1，故参数j的近似取值范围为0.71≤j≤1.1。随着线上市场需求规模变化率j的增大，供应链三方成员的价格策略均呈现上涨态势。受制于批发价的上升，零售商r选择提高零售价、降低服务水平等策略以减缓收益受损的速度，其市场需求量随之萎缩。而受益于线上市场需求的增大，制造商M1与制造商M2的总需求量均增加，线下需求量被转移到线上市场。伴随着制造商M1产能的递增，制造商M1与制造商M2的生产成本同时上升。从产能分配来看，制造商M1的产能分配逐渐偏向线上市场，以应对线上需求增大导致的线上市场竞争加剧局面。相对于线下市场，线上市场的产能分配比例也逐步增加，从1.341增加至2.291。

此外，参数j2的增大只会影响到制造商M2的需求量及收益，带动两者的增大，而不影响其他参数的变化。

7.1.2 产能优化的三维数值模拟分析

首先本节基于“线上市场容量变化率”与“线下市场容量”两个变量分析产能优化问题。行业电子商务的发展程度直接决定了线上市场容量变化率j的大小，根据上文继续假设ed1＝0.5，j1＝1.5，j2＝1.2， j3＝0.8，可以得到图7－2及附录7－3。观察图7－2可以发现，最优产能决策随线下市场容量ar的增大而增大，随线上市场容量变化率j的增大而增大。然而，当j较低时，最优产能决策随线下市场容量ar的增速明显减缓。随着j逐步变大，增速减缓的速率放慢。这说明在行业电子商务发展程度较低时，扩大线下市场容量、刺激消费将增加供应链的最优产能决策，但这种增速比较缓慢。随着行业电子商务前进步伐的加快，刺激线下市场容量的增加，将明显增加供应链的最优产能值。此时供应链最优产能决策的增速效应变大了。

其次，观察后文附录7－3，发现当线上市场容量变化率j较小时，制造商M1的线上需求量随线下市场容量ar的增大而降低。然而j增大时，制造商M1的线上市场需求量随线下市场总需求量ar增大而增大。这说明，在行业电子商务发展程度较低时，零售商r是制造商M1线上直销的主要竞争对手，制造商M2还不具备显著竞争力。此时线下市场容量ar增大会进一步增强零售商r的竞争力，而线上市场容量ae的增大对线上市场需求增加的影响不大，不过制造商M1的线上市场需求量减速将放缓。进一步地，在行业电子商务发展程度较高时，制造商M1与M2的线上市场需求均随线下市场容量ar的增大而增大，随线上市场容量ae的增大均加速增大。线上市场上制造商M1与制造商M2竞争激烈。

第三，当线上市场容量变化率j较小时，零售商r的市场需求量随ar增大而增大。然而j增大时，零售商r的市场需求量随ar增大而降低。这与第二点的理由是一致的。在行业电子商务发展程度较低时，零售商r是制造商M1线上直销的主要竞争对手，线下市场容量ar增大会显著增强零售商r的竞争力，而线上市场容量ae的增大对零售商r需求量的影响不大，不过零售商r需求量的增速将放缓。进一步地，在行业电子商务发展程度较高时，线下市场总需求量ar的增大对提升零售商r竞争力的正向效应有限，线上市场容量ae的增大进一步减轻了这种正向效应，线下市场的潜在需求群体迁移至线上市场。

第四，关于线上线下市场的产能分配问题，在下节会详述。观察附录7－3发现，无论是制造商M1还是线上市场整体，随着线下市场容量ar及j的增加，线上市场的产能分配比例明显上升。单独提升两者其一均会带来线上市场产能分配比例的增加。而制造商M1总产能与制造商M2的产能分配比例，随着线下市场容量ar及j的增加，制造商M1的产能相对于制造商M2明显下降，源于线上市场容量上升带来的制造商M2竞争力急速上升，制造商M1的主导地位受到挑战，基于行业电子商务的发展现状，这种情形模型三暂不考虑。

图7－2 行业电子商务发展程度影响下的最优产能决策变化规律

7.1.3 双因素作用边界范围的数值分析

随着行业电子商务发展程度的提高，其线上市场容量发生变化。而行业竞争的加剧、新竞争对手的进入、产品创新的突破等也会导致线下市场的容量发生改变。“线上市场容量变化率”与“线下市场容量”双因素的变化如何决定了供应链的产能优化决策。假设ar≤2 000，可以找出“线上市场容量变化率”与“线下市场容量”双变量影响下的边界范围，即固定参数j，找出线下市场容量ar的取值范围，进一步找出线上市场容量变化率j的取值范围，如下表7－1所示。

表7－1 参数赋值下供应链产能决策的约束条件

续 表

首先，通过观察表7－1发现线上市场容量变化率j的边界范围为0.54≤j≤1.112 694。这意味着在已知参数赋值条件下，无论线下市场容量如何改变，线上市场容量占线下市场的比例存在固定边界范围，即0.54≤j≤1.112 694。若“行业电子商务发展程度”脱离边界范围以外，则模型研究没有意义。(www.daowen.com)

第二，当行业电子商务发展程度一定时，线下市场容量的增减会影响某些变量的走向，详见附录7－3。图7－3将情形一与情形二相结合，在j＝0.65时，0≤ar≤2 000范围内曲线（p1－ w）呈现上凹形状，其中213.52≤ar≤1 776.42区间函数（ p1－w）为负值。说明在行业电子商务发展程度较低时，即区间201.814≤ar≤213.52内，函数（p1－ w）逐步降低，制造商M1与M2的线上直销价格均下降，零售商r的线下市场售价增大。制造商M1的产能分配逐步偏向线下市场，行业产能整体也逐步向线下市场偏移，制造商M1的行业产能比重明显增加，最优产能决策增加。反之，在1 776.52≤ar≤2 000时，函数（p1－ w）逐步增加，制造商M1的线上市场优势逐渐增加，最优产能决策增加，其产能分配逐步偏向线上市场，行业产能整体也向线上市场偏移，制造商M1的行业产能比重明显减少。这进一步揭示出，在行业电子商务发展程度较低时，线下市场容量很高的行业，更适合开展线上市场业务，线上市场竞争更激烈，制造商M2的生存空间更大。反之线下市场容量较低的行业，其线上市场竞争力则较弱。

图7－3 p1－w的变化规律（情形一与情形二）

第三，曲线（pr－p1）在情形一至情形四中均呈现出单调递增趋势，表示在行业电子商务发展程度不太高时，线下市场容量的增大对线上消费者更为有利，从线上市场购物能够获得更多的福利。然而，当线上市场容量变化率j变大如情形五所示，曲线（pr－p1）呈现出下凹形状。这意味着当行业电子商务程度较高时，线下市场容量的增大使得线上消费者福利（pr－p1）呈现出先多后少的规律。而在ar＜202.587或ar＞770.213两种情形下，将会出现pr≤p1的情形。随着线上市场竞争的加剧，越来越多的年轻化消费者对线上市场购物已经形成依赖性消费，而线下市场迫于竞争压力加大促销力度，某些行业如日用品等已经存在pr≤p1的现象。

第四，在行业电子商务程度较高时（如情形五），制造商M1的短期生产成本曲线呈上凹状，即曲线存在最低点。这意味着虽然线下市场容量的调整难度较大，但制造商M1可以通过调整渠道或品牌促销水平（ed1或eb1）等措施来尽量使得c1曲线达到最低点。并且，此时曲线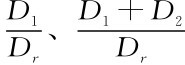均呈现出上凹状，曲线呈现下凹状。这意味着在行业电子商务程度较高时，随着线下市场容量的增大，线上市场的竞争力呈现出先弱后强的特点，制造商M1的产能分配也如此，这与其短期生产成本c1曲线的特点有内在一致性。说明了线上市场竞争力的爆发能力较强。进一步地，行业产能分配曲线的下凹状进一步验证了线下市场容量的增大，对线上市场竞争力具有正向效应，制造商M1的行业产能所占份额由增速减缓变为减速下降，而制造商M2的行业产能所占份额则呈现相反规律。

7.1.4 风险防范之产能过剩、不足与缺货的数值分析

基于7.2.1的基准值，即 ＝0.5，且假设j＝1，j1＝1.5，j2＝1.2，j3＝0.8，得到K＊＝416＞250，如表7－2与表7－3第一栏所示。

表7－2 模型三产能优化的数值模拟分析

制造商M1的最优产能决策显示出其短期产能处于不足状态。此处，短期产能不足的含义是，制造商M1的最优产能决策K＊＝416高于其总生产成本ATC的最佳生产能力K0＝250，反之则是产能过剩情形。而制造商M1缺货的含义，既可以是产能过剩下的缺货，也可以是产能不足下的缺货。基于上文假设分析当制造商M1暂时缺货，如上游供应商出现质量问题、原材料不足等问题，而制造商M2不受影响即其生产成本c2＝6.661不变时，供应链竞争体现出来的规律。

表7－3 缺货与产能不足加剧的数值分析（续）

第一种缺货情形为制造商M1暂时缺货，变量为j3和ed1，其他参数赋值不变。此时制造商M1的产能由K＊＝416的最佳状态降为K＊＝400时，生产成本c1随之由9.52降为8.5，促销努力ed1由0.5降为0. 423 2。此时如果制造商M1与M2继续展开线上市场的促销竞争，在假设M1与M2的线上品牌促销努力变化率不变时，制造商M2需要付出远甚于制造商M1的线上渠道促销努力，才能维系竞争的平衡，见表7－2与表7－3第二栏所示。线上市场的促销竞争提升了制造商M1与M2的需求量，降低了零售商r的线下市场需求量，行业产能分配整体偏向线上市场，制造商M1的线上市场产能分配比例变大。因此促销努力越大，越能激励制造商M2扩大产能，缓解由于制造商M1缺货带来的供应短缺。

第二种缺货情形为制造商M1短期急剧缺货，变量为K＊与ed1，其他参数赋值不变。当制造商M1的产能从400降为150时，观察表7－2与表7－3第三栏可以发现，以K＊＝250为分水岭，传统零售商r的零售价pr先降后升，收益与需求量均先升后降；制造商M1的零售价p1先升后降，收益与需求量均先降后升，制造商M1的产能分配比例也先降后升；制造商M2的零售价p2先升后降，收益与需求量均先降后升。且随着制造商M1缺货程度的加大，出现了pr＜p1的情形。这意味着高额缺货将导致制造商M1抬高线上市场的售价，在稀缺性产品等行业可能出现这种情形，而传统零售商r的收益显著上升。

第三种情形，属于制造商M1短期产能不足情形下的产量进一步扩大，产能不足加剧，属于低水平过度扩张情形。变量为K＊与ed1，其他参数赋值不变。随着制造商M1的产能从400逐步递增，线上促销努力ed1同步递增，的数值逐渐减小。虽然线上市场促销的强化提升了制造商M1与M2的需求量、总收益，降低了零售商r的线下市场需求量、总收益，但制造商M1的生产成本c1由9.52升至10.1，明显处于边际收益递减的低效率状态。产能不足的现状迫使制造商M1进一步扩大规模，降低单位生产成本，如图7－4所示。

图7－4 模型三下制造商M1的长期生产成本曲线

图5－2的短期生产成本曲线ATC对应为图7－4的SATC1，阴影区域为前文的研究重点，可以看出点处于严重的短期产能不足位置，制造商M1急需扩大规模，将SATC1向前推进至SATC2，曲线LATC为制造商M1的长期生产成本曲线。由经济学相关理论可知，在长期生产成本曲线LATC上，各短期生产成本曲线的曲线变化率α通常假设不变，会改变的多是β与K0。且由于短期生产成本曲线逐步向右向下移动，最终使得长期生产成本曲线LATC呈现出上凹的二次曲线形态。

前文短期生产成本曲线SATC1面临突然缺货时，由于初始最优状态为产能不足，点严重偏右，少量缺货反而使得短期生产成本下降，产能回归到合理的状态。从表7－3、7－4第三栏数据可以看出，当产能降为250时，制造商M1的线上渠道促销努力最小，线上需求量最低，批发价格最低，线上直销价格最高，总收益最高（排除产能严重不足或过剩情形）。零售商r的线下售价最低，服务水平最高，线下需求量最高，线下收益最高。制造商M2的线上需求量最小，线上直销价格最高，总收益最低。制造商M1的线上产能分配比例最小，线上市场的产能分配比例最小。供应链博弈在制造商M1产能为250时达到最佳均衡状态。

随着制造商M1扩大产能的要求提高，短期生产成本曲线SA T C1逐步向右下移动。图7－4中当变为时，供应链博弈达到长期均衡的理想状态，效率实现最优。