随着电子商务日趋成熟和规范化，B2B和B2C交易活动已成为制造企业未来的发展战略重心之一，比如服装、玩具、日用品、钢铁等行业。已经在线下市场占据主导地位的强势制造商M1，与仅仅分享线上市场份额的弱势线上制造商M2之间的竞争，将随着线上促销形式的丰富而愈发激烈，这进一步增加了供应链的博弈复杂程度，拓宽并加深了线上线下市场供应链研究的既有规律。基于第三章的模型一，本节模型三增加进促销努力水平因素，具体描述如下：

一个强势的传统企业M1（制造商M1）及其线下零售商r（零售商r）和一个弱势的网络品牌制造商M2（制造商M2）构成的供应链结构上，制造商M1在线下市场拥有成熟的销售渠道，用一个集成性的零售商r代表，它是制造商M1的博弈追随者，处于供应链三方博弈的次主导地位。线上市场的弱势线上制造商生产制造商M1的替代性产品，以相对低廉的价格吸引线上线下市场消费者的眼球。用一个集成性的网络品牌制造商M2代替，制造商M2为供应链博弈最弱方，这与多数实际情形一致。

线上消费者具有分散化、自主性强等特点，丰富的网络广告形式更为线上企业带来了多样化的促销方式。制造商M1的线上促销努力分为两个维度，线上渠道促销努力水平ed1和线上品牌促销努力水平eb1。提高线上渠道促销努力水平ed1能提高消费者的购买意愿，提高线上品牌促销努力水平eb1能提高自身品牌的认可度。同理，制造商M2的线上促销努力，分别为线上渠道促销努力水平ed2和线上品牌促销努力水平eb2。零售商r也将提升零售服务水平以应对线下消费者的流失，其促销努力水平用er表示。如图5－8所示。

图5－8 模型三：零售商r次主导下的基本模型（考虑促销因素）

制造商M1在市场竞争中积累了丰富的行业经验，已经成为线上线下市场内的领军企业，零售商r作为制造商M1的忠实追随者，亦已经成熟壮大，占据博弈的主导地位。制造商M1又拥有对零售商r批发价格的主导权。制造商M2摆脱了构建线下市场渠道的高额成本困扰，凭借渠道、品牌促销等多种手段致力于在线上市场发掘出自己独有的网购消费群体，与制造商M1共同分享线上市场份额。与3.1的模型特点类似，在该供应链结构上，制造商M1为保证线下市场的销售渠道，仍为零售商r的上游供应商。同时，制造商M1和制造商M2在线上市场展开竞争，争夺线上市场的份额。而且，线上市场上制造商M1与M2作为一个整体，成为线下零售商r的竞争对手。本书假设制造商M1与M2在线上市场统一采取直销模式。

另一方面，为了获得更多的线下市场份额，零售商提供附加服务er （er＞0）以获取竞争优势，其服务成本为ηe2r／2，η为服务成本系数，η越高则零售商的服务成本越高。零售商的零售价为pr，批发价为w，μ为附加零售服务的边际需求，即服务需求弹性。零售商的附加服务越丰富，吸引来的消费者需求就越旺盛。由于制造商M1、制造商M2及零售商r在线上与线下市场的促销活动将改变消费者对不同市场的认可度，进而影响到线上线下市场的需求改变。渠道促销努力水平ed1、ed2、er会影响到线上与线下市场的消费者需求量，而品牌促销努力水平eb1、eb2仅影响到线上市场的需求量。制造商M1、制造商M2及零售商r的需求函数分别为

D1（p1，w，ed1，eb1）＝［ae－mp1＋np2＋θ（pr－p1）＋γed1－λed2－φ（er－ed1）］eb1

D2（p2，ed2，eb2）＝［ae－mp2＋np1＋θ（pr－p2）＋γed2－λed1－φ（er－ed2）］eb2

Dr（pr，er）＝ar－mpr＋θ（p1－pr）＋θ（p2－pr）＋γer＋φ（er－ed1）＋φ（er－ed2）

线上市场放大了线下市场的需求空间，制造商M1的过剩产能有了新的释放空间，产能不足时的分配决策亦重新考虑，产能优化策略的传统理念被颠覆。根据经济学原理的短期成本理论观点，制造商M1的短期生产成本曲线符合下图5－9所示。曲线M C表示平均边际生产成本，曲线AVC表示平均变动生产成本，曲线ATC表示平均总生产成本。可变成本可以调整，而固定成本如厂房、设备等不能调整。根据边际收益递减的规律，最初MC曲线由于规模效应的存在，随着产量的增大而降低，曲线AVC下降。在产量到达一定的规模后，若固定投入保持不变，则终将构成生产制约因素，曲线AVC将开始上升，曲线MC开始上升，曲线ATC呈现出先降后升的特点，在U形ATC曲线底部K0处，满足条件为MC＝ATC＝min（ATC）。据此假设制造商M1的A TC曲线具备近似下凹的二次函数特征，表达式为c1（K） ＝α（K－K0）2＋β，α＞0，β＞0。其中产能K的含义，为制造商M1在线上线下市场为满足需求而生产的产量。参数α代表生产规模一定（如固定成本如厂房、设备等规模一定）下，平均总生产成本曲线ATC随产量增加的变化比率，α越大则变化速率越快，对应曲线ATC的上凹程度就越高，反之越低。K0为制造商M1在正常生产条件下所能达到的最佳生产能力，而参数β＝min（ATC）表示曲线ATC在达到最佳生产能力K0时的总生产成本。当最佳生产能力K0超出实际产量K达到一定程度时即称之为产能过剩，反之称之为产能不足。产能过剩的出现一般伴随着价格下跌、利润减少甚至亏损。

当产能过剩或不足时，供应链的长期产能决策面临调整。短期总生产成本曲线ATC向长期生产成本曲线LTC过渡时，随着K0的增大及参数β的降低，曲线ATC逐步向右向下移动，最终使得长期生产成本曲线也呈现近似下凹的二次曲线形态，后文会详述。

图5－9 制造商M1的短期生产成本曲线

5.2.1 模型三的基本假设

1.符号含义

Di（i＝1，2，r）：分别表示制造商M1的线上市场需求、制造商M2的线上市场需求及零售商r的线下市场需求，亦表示各自的产能。

pi（i＝1，2，r）：分别表示制造商M1的线上直销价格、制造商M2的线上直销价格，以及零售商r的线下市场销售价格。

πi（i＝1，2，r）：分别表示制造商M1的总收益（包含线上直销收益与线下收益）、制造商M2的总收益（即线上直销收益），以及零售商r的线下市场总收益。

K：制造商M1的产能，表示在线上线下市场为满足需求而生产的产量。

c1，c2：分别表示制造商M1和M2的生产成本。

w：制造商M1的线下市场批发价格。

er：零售商r的线下渠道促销努力水平。

ae，ar：分别表示产品的线上与线下市场的总容量，并分别反映了该类产品线上与线下市场的总需求潜力。参数ae表示产品i（ i＝1，2）的线上市场“综合顾客需求基数”，反映该类产品对网络购物者的内在吸引力，ar表示线下市场的顾客内在需求，反映出该类产品在线下市场所处的发展水平。

a：为线上与线下两个市场的总容量之和，反映了该类产品的市场总体发展水平，ae＋ar＝a。

m，n：对竞争产品价格的反应。参数m表示顾客需求对产品价格的反应，参数n表示顾客需求对竞争产品价格的反应。

θ：线下与线上市场间的需求扩散程度，θ＞0。

F：零售商r的店铺租金等成本，F＞0且为常数。

2.假设条件

（1）一个强势品牌制造商M1占据博弈主导地位，零售商r为博弈次主导方，弱势线上制造商M2为博弈地位最弱方。

（2）线上市场需求与线下市场需求彼此相关，线上与线下市场的信息完全透明。

（3）制造商M1的A T C曲线服从近似下凹的二次函数，c1＝＋β，α＞0，K0为制造商M1在正常生产条件下所能达到的最佳生产能力，β＝min（ATC）＞0。

（4）制造商M1与制造商M2在线上市场均采取线上直销模式。

（5）制造商M2没有线下市场的销售渠道，线下市场保持着被零售商垄断的格局。故eb1仅对线上市场需求的变化有影响。同理，eb2亦仅影响到线上市场需求的变化。

（6）线上市场的渠道促销成本分别为函数f（ ed1）＝κed1，f（ ed2）＝κed2，且满足f′（ed）1 ＝f′（ed）2 ＝κ，ed1≥0，ed2≥0，κ＞0且为常数。零售商r的线下市场促销成本为f e（）r 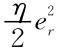＝（er≥0），且满足f″（er）＝η，η＞0且为常数。

（7）线上市场的品牌促销成本分别为函数f（ eb1）＝ωeb1，f（ eb2）＝ωeb2，且满足f′（eb）1 ＝f′（eb）2 ＝ω，ω＞0且为常数，eb1≥0，eb2≥0。

（8）p2＞c2，p1＞w＞c1，否则零售商r将放弃在线下市场向制造商M1采购，转而到线上市场批发，这不符合本书的基本假设。

（9）pr＞p1，即线下市场的产品零售价高于线上的产品零售价，这与实际情形基本一致。

（10）m＞n＞0，即消费者需求关于自身产品价格变化的反应，比对竞争对手产品价格变化的反应要大。

（11）γ＞λ＞0，即消费者需求关于自身产品线上渠道促销努力水平变化的反应，比对竞争对手产品的线上渠道促销努力水平变化的反应要大。

线上线下市场并存下，考虑促销投入竞争因素使得制造商M1、制造商M2及零售商r三方企业的博弈活动变得更为复杂。促销投入因素使得定价决策可能会出现逆反，即线下市场的定价决策低于线上市场的定价决策。线上线下市场博弈的顺序详述如下：首先，制造商M1与零售商r展开主从对策博弈，制造商M1为博弈主方，零售商r为博弈从方，决定各自的销售价格、批发价格、服务水平等；然后，制造商M2作为“制造商M1—零售商r”的博弈从方，决定自己的线上市场直销价格。

模型三的研究重点在于，寻找出制造商M1、制造商M2及零售商r的最优决策存在条件，及供应链协调的实现条件，并通过数值分析深入探讨制造商M1与零售商r的相关参数变化时，供应链各方最优决策将受何影响。

5.2.2 制造商M2的收益函数

根据收益函数

π2＝（p2－c2）D2－f（ ed2）－f（ eb2）＝（p2－c2）［ae－mp2＋np1＋θ（pr－p2）＋γed2－λed1－φ（er－ed2）］eb2－f（ ed2）－f（ eb2）

对其进行寻优求导，有

根据一阶条件为零可以得到

D2－（p2－c2）eb2（m＋θ）＝0

2 （m＋θ）p2＝np1＋θpr＋［ae＋（γ＋φ）ed2－λed1－φer］＋（m＋θ）c2

又有

当（p2－c2）［ae－mp2＋np1＋θ（pr－p2）＋γed2－λed1－φ（er－ed2）］＞κ时，π2随eb2单调递增，反之单调递减；

当（p2－c2）（γ＋φ）eb2＞κ时，π2随ed2单调递增，反之单调递减。

故可以得到如下定理：

定理5.1 线上线下市场并存下且考虑促销因素时，若线下零售商r处于次主导地位，弱势线上制造商M2不退出竞争需要满足的条件为，(www.daowen.com)

推理5.1 线上线下市场并存下且考虑促销因素时，若线下零售商r处于次主导地位，当满足条件（p2－c2）（γ＋φ）eb2＞κ时，制造商M2的收益随变量ed2增大而单调递增；当满足条件（p2－c2）［ae－mp2＋np1＋θ（pr－p2）＋γed2－λed1－φ（er－ed2）］＞κ时，制造商M2的收益随变量eb2增大而单调递增。

5.2.3 零售商r的收益函数

零售商r的利润函数为

πr（pr，er）＝ （pr－ w ）Dr（pr，e）r－f （er）－F＝（pr－w）［ar－mpr＋θ（p1－pr）＋θ（p2－pr）

根据前面方程（5－1）可以推得

令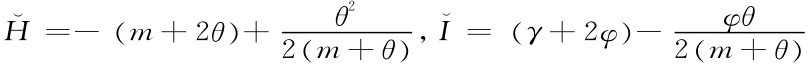，则当即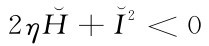时，零售商r存在最优收益。由此可以得到定理5.2：

定理5.2 线上线下市场并存下且考虑促销因素时，若线下零售商r处于次主导地位，线下零售商r必存在最优定价决策的条件为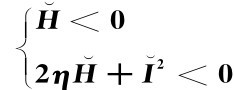。此时零售商r的最优收益值为正值，也就是说，此时零售商r才有动力参与线上线下市场竞争。

又根据一阶条件为零，化简得到方程组

联立方程组（5－4）与（5－1），可以得到

令ae＋γ＋（）φed2－λed1＝，，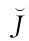

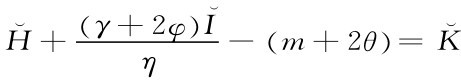进一步化简得到

再令

则变为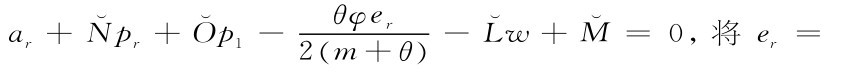代入可得

化简得到

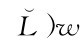继续令，则，简化得到

5.2.4 制造商M1的收益函数

已知制造商M1的收益函数为π1＝（p1－c1）D1＋（w－c1）Dr－f（ ed）1 －f（ eb）1 ，即

π1＝（p1－c1）［ae－mp1＋np2＋θ（pr－p1）＋γed1－λed2－φ（er－ed1）］eb1＋（w－c1）［ar－mpr＋θ（p1－pr）＋θ（p2－pr）＋γer＋φ（er－ed1）＋φ（er－ed2）］－f（ed1）－f（eb1）

首先对变量p1进行寻优求导，根据前面公式（5－1）、（5－4），可以得到

且为制造商M1有最优收益的必要条件之一。

其次对变量w进行寻优求导，根据前面公式（5－1）、（5－4），可以得到

由此可以推得制造商M1有最大收益的充要条件为

得到定理5.3：

定理5.3 线上线下市场并存下且考虑促销因素时，若线下零售商r处于次主导地位，制造商M1必定存在最优定价决策的条件为

接着寻找最优变量，通过求解如下方程组

可以寻找出最优变量p＊1和w＊，将其代入前面（5－1）至（5－5），可以进一步求得其他最优变量值，以及

π＊1＝－（p1－c1）［（p1－c1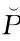）eb1＋（w－c1）］－（w－c1）［（p1－c1）eb1＋（w－c1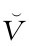）］－f（ed1）－f（eb1）

π＊2（p2）＝（p2－c2）D2－f（ed2）－f（eb2）＝eb2（m＋θ）（p2－c2）2－f（ed2）－f（eb2）

π＊r（pr，er）＝－（pr－w）2－f（er）－F

各最优变量结果详见下表5－1所示。

表5－1 模型三的最优变量结果

续 表

下面进一步寻找最优变量的存在条件及分析、单调性变化等。根据表5－1可以得到以下几点结论：

第一，品牌促销努力水平eb2不影响各项最优变量，但会影响到制造商M2的最优收益。

第二，F作为判断条件，仅与强势制造商M1的品牌促销水平eb1有关。与其他促销水平均无关。

第三，由于零售商r没有考虑到单位产品的店面租金等问题，故导致零售商r在较低价格下也会进行销售，如果考虑进租金问题，零售商r的生存空间就微乎其微了。这种情形下，如果要扶持和鼓励零售商r来维持线下市场的话，强势制造商M1就应该采取对应措施。

5.2.5 “制造商M1—零售商r”供应链协调

若“制造商M1—零售商r”供应链协调存在，此时需要寻求各项最优变量。根据逆向归纳法，供应链三方成员的博弈进程变为，“制造商M1—零售商r”的供应链整体与制造商M2展开主从对策博弈。我们把所有最优决策变量下标添加字母T，以示与上文相区别，譬如pi T，edi T，ebi Ti＝（1，2），er T，w T等。根据逆向归纳法，可得

当≥0时，制造商M2的最优收益与ed2 T正相关，反之则反相关；eb2 T与制造商M2收益的关系同理可得。“制造商M1—零售商r”的供应链整体收益函数为

πs＝（p1 T－c1）D1（p1 T，w T，ed1 T，eb1 T）＋（pr T－c1）Dr（pr T，er T）－f（ed1 T）

求导可以得到，

继续，“制造商M1—零售商r”供应链的收益函数为

πs（p1 T，pr T，er T）＝（p1 T－c1）D1 T＋（pr T－c1）Dr T

并且，

当＞0时，πs随ed1 T单调递增，反之则单调递减

＋γed1 T－λed2 T－φ（er T－ed1 T）］－κ

当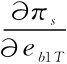＞0时，πs随eb1 T单调递增，反之则单调递减

且此时，

下面联立方程组，有

根据方程组可以求解出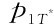、、、等最优变量及各项最优收益。并得到如下定理5.4：

定理5.4 当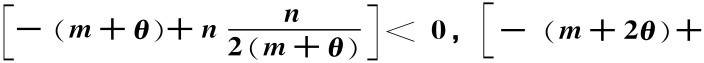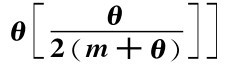＜0，且同时成立时，存在“制造商M1—零售商r”的供应链协调。