传统线下市场，一个集成性的强势品牌制造商M1（以下简称制造商M1）及其线下市场集成零售商r（以下简称零售商r），与其在线上市场的集成性弱势线上制造商M2（以下简称制造商M2）展开竞争。制造商M1在线下市场拥有成熟的销售渠道，用一个集成性的零售商r代表，它是制造商M1的博弈追随者，如图3－1所示。

随着电子商务实施程度的提升，线上市场出现了众多的弱势线上制造商，它们生产可以替代制造商M1的同质同类产品，并进行线上多渠道销售。制造商M2不必受制于线下市场高昂的渠道构建成本、地域障碍等，以相对低廉的价格吸引线上线下市场消费者的眼球。制造商M2为供应链博弈最弱方，这与目前我国多数行业的实际情形一致。

图3－1 模型一：零售商r次主导下的基本模型（不考虑促销因素）

无论在线上或线下市场，制造商M1和零售商r均为该行业的领军企业，其中制造商M1又拥有对零售商r批发价格的主导权。另外，随着线上市场的日趋成熟，制造商M2发现了网络直销的商机，可以摆脱构建线下市场的高额成本困扰，且能够发掘出自己独有的网购消费群体，故加入线上市场竞争，与制造商M1共同分享线上市场份额。

制造商M1的角色变得复杂。一方面，制造商M1为保证线下市场的销售渠道，将保持为零售商r的上游供应商。另一方面，制造商M1和M2在线上市场展开竞争，争夺线上市场的份额，线上市场上制造商M1与M2又成为线下零售商r的竞争对手。本书假设制造商M1与M2在线上市场均采取直销模式。

为了获得更多的线下市场份额，零售商可以通过提供附加服务v（v＞0）来获取竞争优势，其对应的服务成本为ηv2／2，η为服务成本系数，反映了零售商提供附加服务导致的成本高低，η越高则零售商的服务成本越高。零售商的零售价为pr，批发价为w，μ为附加零售服务的边际需求，即服务需求弹性。零售商的附加服务越丰富，如地点便利性、舒适的购物环境、良好的售后服务、包装等因素，其吸引来的消费者需求就越旺盛。三者的需求函数分别为

D1（p1，w）＝ae－mp1＋np2＋θ（pr－v－p1）

D2（p2）＝ae－mp2＋np1＋θ［（pr－v）－p2］

Dr（pr，v）＝ar－mpr＋μv＋θ［（p1＋v－pr）＋（p2＋v－pr）］

3.1.1 符号含义

Di（i＝1，2，r）：分别表示制造商M1的线上市场需求、制造商M2的线上市场需求及零售商r的线下市场需求，亦表示各自的产能。

pi（i＝1，2，r）：分别表示制造商M1的线上直销价格、制造商M2的线上直销价格，以及零售商r的线下市场销售价格。

πi（i＝1，2，r）：分别表示制造商M1的总收益（包含线上直销收益与线下收益）、制造商M2的总收益（即线上直销收益），以及零售商r的线下市场总收益。

K：制造商M1的产能，表示在线上线下市场为满足需求而生产的产量。

c1，c2：分别表示制造商M1和制造商M2的生产成本。

w：制造商M1的线下市场批发价格。

er：零售商r的线下渠道促销努力水平。

ae，ar：分别表示产品的线上与线下市场的总容量，并分别反映了该类产品线上与线下市场的总需求潜力。参数ae表示产品i（i＝1，2）的线上市场“综合顾客需求基数”，反映该类产品对网络购物者的内在吸引力，ar表示线下市场的顾客内在需求，反映出该类产品在线下市场所处的发展水平。

a：为线上与线下两个市场的总容量之和，反映了该类产品的市场总体发展水平，ae＋ar＝a。

m，n：对竞争产品价格的反应。参数m表示顾客需求对产品价格的反应，参数n表示顾客需求对竞争产品价格的反应。

θ：线下与线上市场间的渠道扩散程度，θ＞0。

3.1.2 假设条件

（1）一个强势品牌制造商M1占据博弈主导地位，零售商r为博弈次主导方，弱势线上制造商M2为博弈地位最弱方。

（2）线上市场需求与线下市场需求彼此相关，线上与线下市场的信息完全透明。

（3）制造商M1的ATC曲线服从近似下凹的二次函数，c1＝α（K－K0）2＋β，α＞0，K0为制造商M1在正常生产条件下所达到的最佳生产能力，β＝min（ATC）＞0。

（4）制造商M1与M2在线上市场上均采取线上直销模式。

（5）制造商M2没有线下市场的销售渠道，线下市场保持着被零售商垄断的格局。

（6）零售商r的线下市场促销成本为（er≥0），且满足f″（er）＝η，η＞0且为常数。

（7）p2＞c2，p1＞w＞c1。否则零售商r将放弃线下市场上从制造商M1采购，转而到线上市场批发，这不符合本研究的基本假设。

（8）pr＞p1，即线下市场的产品零售价高于线上的产品零售价，这与实际情形基本一致。

（9）m＞n＞0，即消费者需求关于自身产品价格变化的反应，比对竞争对手产品价格变化的反应要大。

线上线下市场博弈的顺序详述如下：首先，制造商M1与零售商r展开主从对策博弈，制造商M1为博弈主方，零售商r为博弈从方，决定各自的销售价格、批发价格，服务水平等；然后，制造商M2作为“制造商M1—零售商r”的博弈从方，决定自己的线上市场直销价格。本章的研究重点在于，寻找出制造商M1、制造商M2及零售商r的最优决策存在条件，及供应链协调的实现条件。继而通过数值分析深入探讨制造商M1与零售商r的相关参数变化时，供应链各方最优决策将受何影响。

3.1.3 制造商M2的利润函数

制造商M2的利润函数为

π2（p2）＝（p2－c2）D2（p2）＝（p2－c2）［ae－（m＋θ）p2＋np1＋θ（pr－v）］

求得

由于θ＞0，m＞0为已知假设，故有如下定理成立：

定理3.1 线上线下市场并存下，线下零售商r处于次主导地位时，线上市场的弱势线上制造商M2能够实现收益最优化。

推理3.1 弱势线上制造商M2的成本越高，线上市场的综合顾客需求基数越大，制造商M2的最优定价则越高。

3.1.4 零售商r的利润函数

零售商r的利润函数为

πr（pr，v）＝（pr－w）Dr（pr，v）－ηv2／2＝（pr－w）［ar－（m＋2θ）pr＋θ（p1＋p2）＋（μ＋2θ）v］－ηv2／2 　（3－2）

其中，

Dr（pr，v）＝ar－mpr＋μv＋θ（p1＋v－p）r＋θ（p2＋v－p）r＝ar－（m＋2θ）pr＋θ（p1＋p2）＋（μ＋2θ）v

而根据方程（3－1）可以推出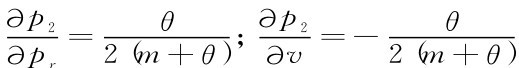，，故由方程（3－2）进一步推得

根据函数πr（pr，v）存在极大值的条件可知，零售商r存在最大收益值应满足恒成立。此时应满足一阶条件

故可以得到

化简为

为了便于观察和发现规律，此处令

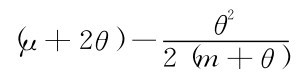，则方程（3－3）变为(www.daowen.com)

下面再对变量v展开求导，有

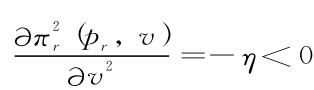恒成立，据函数πr（pr，v）存在极大值。此时一阶条件应满足

得到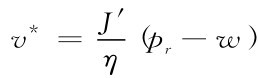，代入方程（3－4）进一步得到

化简得到

进一步将其代入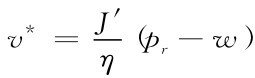，可以得到

故求得最优变量为

且得到如下定理3.2，

定理3.2 线上线下市场并存下，线下零售商r处于次主导地位时，其实现最优决策的条件是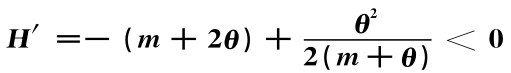，恒成立。

3.1.5 制造商M1的利润函数

制造商M1的利润函数为

π1（p1，w）＝（p1－c1）D1（p1，w）＋（w－c1）Dr（pr，v）＝（p1－c1）［ae－（m＋θ）p1＋np2＋θ（pr－v）］＝（p1－c1）［ae－（m＋θ）p1＋np2＋θ（pr－v）］

根据前文所求p＊2、p＊r、v＊的表达式

可以得出

对制造商M1的收益函数进行寻优求导，得到一阶表达式为

其中

故令

二阶表达式为

O′＜0为满足制造商M1获取最优收益的必要条件之一。

进一步地

令

则可以简化为

二阶表达式为

综上分析可以找出，满足制造商M1获取最优收益的充分必要条件为

该充分必要条件可以简化为

定理3.3 线上线下市场并存下，线下零售商r处于次主导地位时，处于主导地位的强势品牌制造商M1存在最优决策的条件为

面可以通过联立方程（3－6）、（3－7），求出各项变量的最优值（如下表3－1所示）。即

表3－1 模型一的最优变量结果

求解该方程组可以得到p＊1、w＊，代入前面所求可以进一步得到p＊2、p＊r、v＊等，且

D＊1＝－（p1－c1）O′－（w－c1）U′，D＊r＝－（p1－c1）Q′－（w－c1）M′

π1（p1，w）＝－（p1－c1）2O′－（p1－c1）（w－c1）L′－（w－c1）2M′

3.1.6 供应链协调的实现条件

若“制造商M1－零售商r”供应链协调存在，此时根据逆向归纳法，仍然先寻找制造商M 的最优决策。

π2（p2）＝（p2－c2）［ae－（m＋θ）p2＋np1＋θ（pr－v］）

得到，

且，

π＊2（p2）＝（m＋θ）（p2－c2）2，D2（p2）＝（m＋θ）（p2－c2）

然后，寻找实现供应链协调条件下“制造商M1－零售商r”供应链的最优决策，此处用πs表示“制造商M1－零售商r”供应链的整体收益，则

πs＝（p1－c1）［a1－（m＋θ）p1＋np2＋θ（pr－v）］＋（pr－c1）［ar－（m＋2θ）pr＋θ（p1＋p2）＋（μ＋2θ）v］－ηv2／2

对其进行寻优求导，则有

令

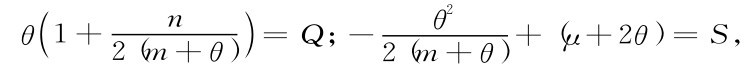则供应链协调的存在条件需满足

此时有

D1（p1，w）＝－［（p1－c1）P＋（pr－c1）Q］　（3－10）

Dr（pr，v）＝－［（p1－c1）Q＋（pr－c1）R］ （3－11）

联立方程（3－9）、（3－10）、（3－11）有

进一步令

则方程组变为

可以求得

定理3.4 线上线下市场并存下，线下零售商r处于次主导地位时，当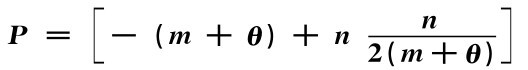＜0，R＝－（m＋2θ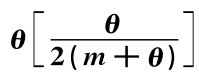）＋＜0，且p＊r＝p＊r T，v＊＝v＊T，p＊1＝p＊1T能够同时成立时，存在“制造商M1－零售商r”的供应链协调。