1.简单的住宅模型

同样，假设如下：

（1）家庭成员只有一人在市中心上班；

（2）家庭成员消费主要到市中心；

（3）居民消费支出包括一般消费品、房屋（含土地）消费和交通消费三类；

（4）所有家庭无差异的，有相同的收入和对土地、交通费、消费品（房屋）的相同偏好，以及均衡下具有相同效用；

（5）上下班时间的机会成本等于零；

（6）环境及公共设施情况城市内各个区域相同。

根据以上的假设，住宅的选址只与距离市中心远近直接相关。居民的收入主要用于购买非土地消费品、地租和交通费用。因此有：

居民收入=非土地消费支出-房租（主要为地租）-交通费用

其中：

非土地消费支出=消费品价格P×消费量Q

交通费用为距市中心距离d 的函数T（d）

地租=土地单位租金R（d）×土地面积S

则居民预算约束函数为

其中：I 为居民收入。

则竞标租金：(www.daowen.com)

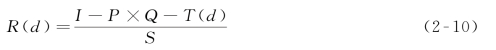
不考虑消费替代，对式（2-10）中距离d 求导，则：

由于T（d）随着距市中心距离的增加，为增函数，即T′（d）＞0，故：

即竞标地租直线为斜向下曲线，随着距市中心距离越远，地租越小。

考虑要素替代，实际上等于同时扩大了居民的收入支付效用，相对提高收入水平。某种意义上就是通过非土地成本的消费，扩大了其支付地租的能力。因此房屋租金函数曲线已经不是原先仅考虑通勤成本下的直线型竞标曲线（图2-11中曲线S1），而是凸向原点的曲线（图2-11中曲线S2），亦即竞标函数具有凸性。

若考虑聚集效应对地租支付能力的影响，则曲线的凸性加剧。聚集效应导致距离城市中心越近，聚集效益越高，企业和居民越愿意向城市中心争得一块立足之地，致使越是靠近城市中心，土地利用越拥挤，土地利用率越高，土地收益也越大，支付地租能力越强。

2.简单住宅模型的变化

如果将简单住宅模型中的假设条件做些改变，则有如下变化（图2-12）。

（1）每个家庭有两人去城市中心上班。则住处距离城市中心近将带来更多的交通成本的节约。均衡状态下，两人挣钱的家庭房屋租金函数将变得更陡。

（2）家庭有经常性的外出消费。则增加了家庭购物和娱乐的交通成本，同样会使家庭房屋租金函数将变得更陡。

（3）考虑上下班的时间成本。上下班的时间是以放弃工作或休闲为代价的。在国外，对上下班的区位研究表明，大多数人以介于1/3～1/2的工资率（每小时工资）来估计上下班时间成本。因此，如果考虑上下班的时间成本，靠近市中心居住能节省更多的上下班成本，对应的房屋租金函数应该更陡。

（4）居民对住房的偏好。如对于大小不同的两个家庭，显然，大家庭对房屋的需求面积大，在两个家庭有相同工资收入的情况下，小家庭可在靠近城市中心处选择小型房屋，支付更高租金，因此小家庭的房屋租金函数更陡。实际上，分析家庭生命周期的不同阶段，可以发现住宅需求的相应规律。

（5）公共服务和税收。公共服务好，税收少，人们愿意付出更高的租金，房屋租金函数更陡。

（6）空气质量和环境。根据城市中心空气和环境质量的不同，房屋租金函数显现不同形态。空气质量好、环境好或房屋质量好、社区环境好等，租金函数均较陡。

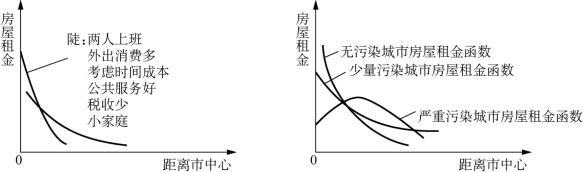
图2-12　房屋租金函数曲线变化比较图