1.经济订货批量模型

经济订货批量（EOQ，即Economic Order Quantity）模型是固定订货批量模型的一种，经济批量模型就是通过平衡订货成本和储存成本，确定一个最佳的订货数量来实现总库存成本最低的方法。根据需要和订货提前期等条件是否确定可分为：确定条件下的模型、概率统计条件下的模型。本书所研究的为确定条件下的模型，因此需要有一些基本的假定条件：

1）只涉及一种商品。

2）年需求量已知。

3）一年之中的需求发生平滑，即需求比例为常数（需求率固定）。

4）订货提前期不变。

5）各批量单独运送接收。

6）没有数量无折扣。

则库存的总费用为库存总费用=订货成本+存储成本+货物成本即库存总费用公式为：

式中T_C——表示一定时期物资库存总费用；

D——表示一定时期库存物资的需求总量；

C——表示物资的单位购买成本或生产成本；

C_R——表示单位物资每次的订货成本；

H——表示一定时期单位物资的储存成本；

Q——表示每次订货的数量。

（1）订货量 对式（8-1）中的Q进行微分求导，并令导数后的方程式得零，可得最佳订货量，即经济批量的基本公式

式中 Q^*——经济订货批量。

则全年订货次数为：N=D/Q （8-3）

每次订货的时间间隔：T=365/N （8-4）

（2）订货点 该模型中假设需求与交货提前期是固定的，而且不允许缺货。因此，订货点就是提前期内的需求，即

R=LTd （8-5）

式中 R——提前期内的需求量；

LT——交货提前期；

d——物资的需求率。

例8-1长城公司是生产某机械器具的制造企业，依计划每年需采购A零件10000个，每次订货成本是100元，每个A零件每年的保管仓储成本是8元。求A零件的经济订货批量，每年的订货次数和每次订货之间的间隔时间。

解：将已知数据代入上述公式中，计算可得经济订货批量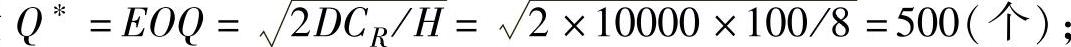

每年的订货次数N=D/Q^*=10000/500=20（次/年）；

每次订货的时间间隔T=365/N=365/20=18.25（天）。

在基本经济批量模型中，作为参数的每次订货成本和单位商品的年储存成本往往难以精确地加以估算。因此需要分析各个参数的变化对总库存成本的影响程度，即需要进行灵敏度分析。如果每个参数的变化对结果的影响很大，则需要对该参数进行非常精确的估算，这样才能计算出正确的经济批量。

上述模型是建立在许多假定基础上的简单模型，如果考虑到实际情况的复杂性，需要对该模型进行修正。下面分别就数量折扣、缺货情况下的购买延后两种情况对该模型进行修正。

2.数量折扣条件下的经济批量模型

在物资采购与供应过程中，供应商为了鼓励采购方多订货，吸引用户一次购买更多的商品，通常会采取某些激励措施诱导采购方订货。其中最常用的措施是按批量大小进行价格折扣，即往往规定对于购买数量达到或超过某一数量标准时给予用户价格上的优惠，给予一定订货价格优惠，如图8-25所示。这个事先规定的数量标准成为折扣点。

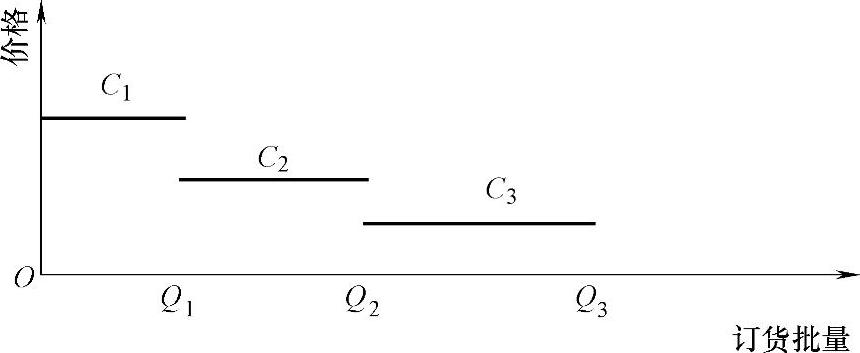
图8-25 数量折扣条件下订货的价格曲线示意图

由于价格随着批量的变化而改变，这样存储成本、订货成本随着价格和数量的变化而变化，因此必须对经济批量模型进行必要的修正。

（1）有数量折扣的确定条件下，储存成本以价格百分比形式表达，经济批量计算步骤如下：

第一步，计算不同区间价格内的经济订货批量(www.daowen.com)

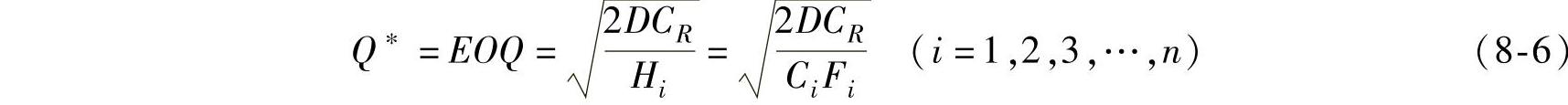
式中 F——储存费率。

第二步，对不同区间价格内的Q^*进行比较取舍。例如已知一个区间内的有关数据如表8-4所示。

表8-4 已知一个区间内的有关数据

若Q^*＜a，则区间内的经济批量Q^*=a；

若a≤订货量≤b，则该区间内的经济批量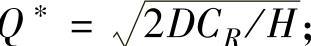

若Q^*＞b，则该区间内没有经济批量。

第三步，计算各区间内对应经济批量的库存总费用T_C（Q_i^*）并进行比较，总费用最小的点对应的数量作为订货批量，得出最佳订货决策。

例8-2某公司准备向某供应商采购一批商品，需求量为30000件，每次订货费为2500元，年保管费率为20%。为激励采购，供应商采用了一定的价格优惠条件，如表8-5所示，试选择合适的订货批量。

表8-5 采购价格表

解：1）求出各个区段的经济订货批量。

根据题意，将已知数据D=30000，C_R=2500，F_i=20%，C_i为单位价格代入式（8-6）计算，可得各个区段的经济订货批量：

Q₁^*=5976，Q₂^*=6283，Q₃^*=6642，Q₄^*=7071，Q₅^*=7596；

2）对不同区间价格内的Q^*进行比较取舍。

由于Q₁^*＞3000，Q₂^*＞5000，所以这两个区间没有经济批量；5001＜Q₃^*＜7000，7001＜Q₄^*＜9000，故Q₃^*和Q₄^*分别是这两个区间的经济批量；Q₅^*＜9000，所以9001是这个区间的经济批量。

3）根据式（8-1）计算三个区间经济批量对应的总库存成本，并进行比较，最小的对应的订货数量为经济批量。

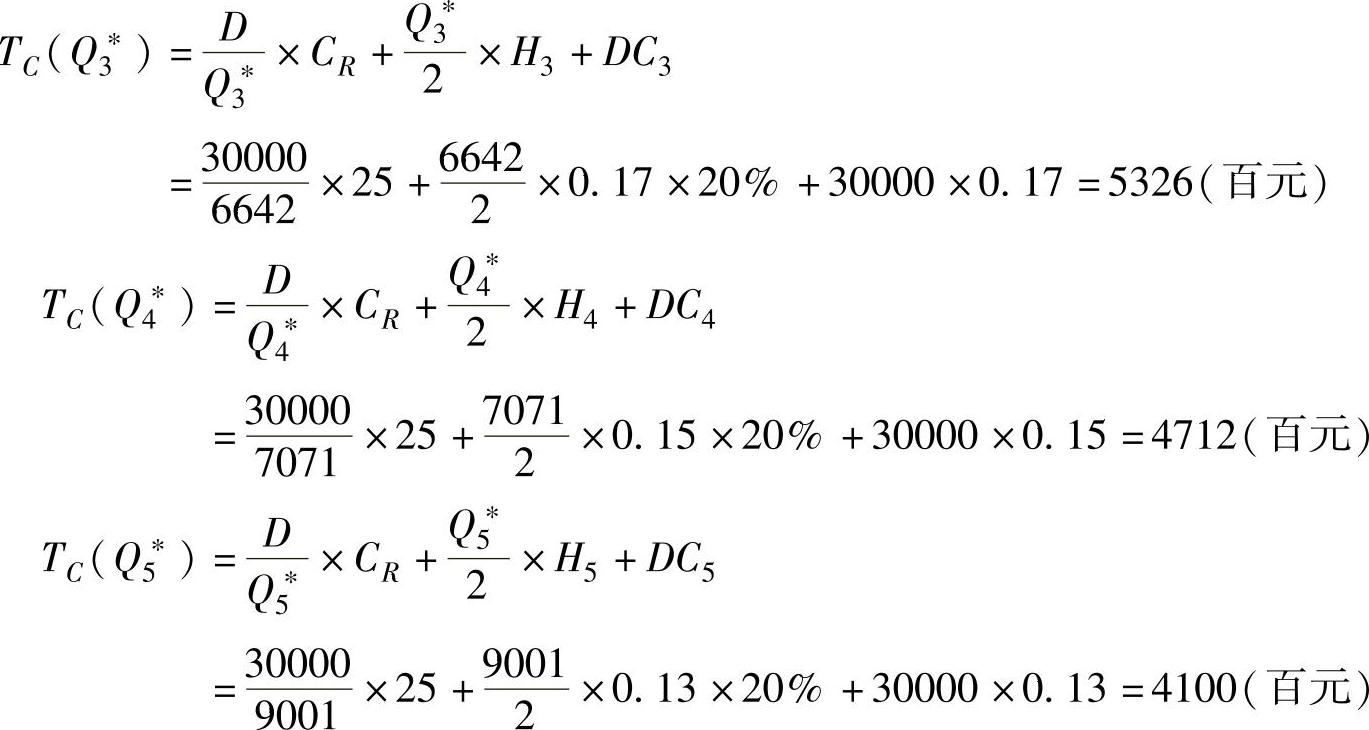
因为T_C（Q₅^*）最小，所以采取Q₅^*=9001作为最佳订货量。

（2）有数量折扣的确定条件下，储存成本为常数，经济批量的计算步骤如下。

第一步，计算通常的经济批量Q^*。

第二步，因为各范围不能重叠，在每个单位价格所对应的可行范围内只能有一个经济批量，标出上步经济批量所对应的范围。

a）若所得经济批量在最低价格范围内，所得经济批量即为最优。

b）若在其他范围内，则以各单位价格所对应的可行数量范围的最小值作为经济批量计算经济批量总库存成本T_C。比较它们，其中总成本最小值对应的数量便是经济批量。

例8-3某配送中心每年为一大型医院配送大约816箱液体清洁剂。订货成本是12元，库存成本是每年每箱4元。新价目表表明，少于50箱的购入成本为每箱20元，50～79箱的是每箱18元，80～99箱的是每箱17元，更大的订货则是每箱16元。请确定经济批量与总成本。

解：1）求出各个区段的经济订货批量。

根据题意，将已知数据D=816，C_R=12，H=4代入式（8-2）计算，可得通常的经济订货批量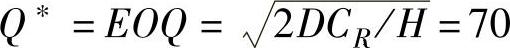：（箱）

2）由于70落在50～79的范围之内，应以18元的单位价格购买。根据式（8-1），以70箱经济批量来计算一年816箱的总成本为

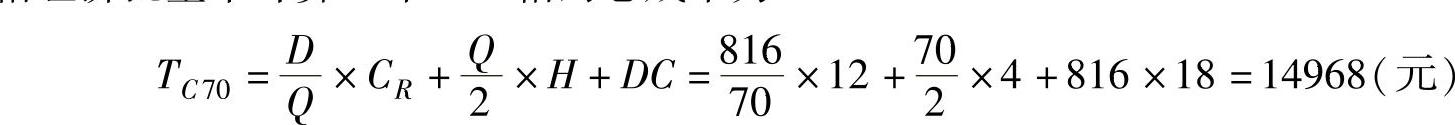
由于存在更低的成本范围，应该再检查一下是否还有比该经济批量成本更低的订货方式存在。因此，分别检查单价17元和16元时的总成本。

为了以17元每箱的价格购买，至少需要每批80箱，则计算其总成本为

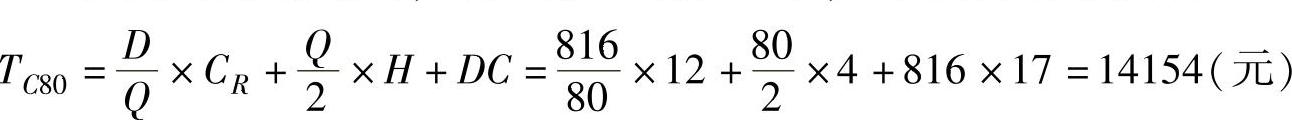
为了以16元每箱的价格购买，至少需要每批100箱，则计算其总成本为

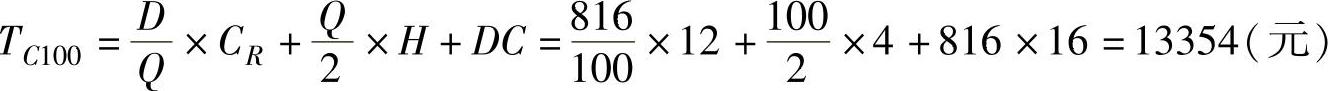
因为T_C100最小，所以100箱作为整个可行范围的经济订货量，总成本为13354元。