配送式运输是指由多个供应点向多个客户的送货运输。它的宗旨是将货物从多个供应点分别送到多个客户手中，既满足客户对货物的配送需要，又满足各供应点存出货要求，并最终做到费用最省。

下面通过例题来说明这类运输问题的求解方法。

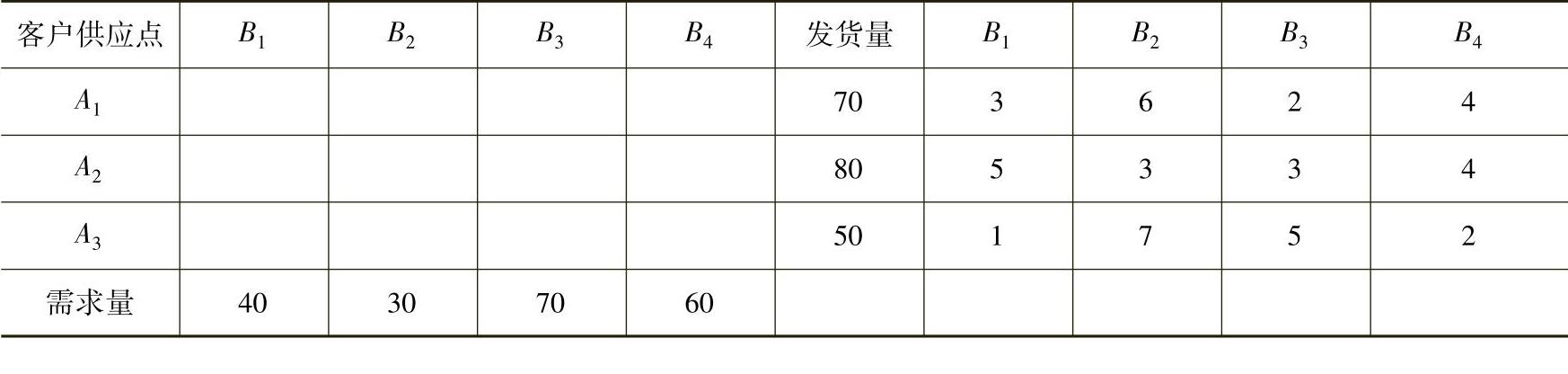
例7-3设有某类物资要从供应点A₁、A₂、A₃供货给客户B₁、B₂、B₃、B₄。各供应点的发货量、各客户的需求量以及从某A_i（i=1，2，3）供给某B_j（j=1，2，3，4）1t货物所需运费见表7-9。问，应如何组织运送才能使总运费最少？

表7-9 （单位：t运价表单位：元/t）

解：第一步，利用西北角法编制初始方案。

（1）首先在表7-9中左上角的空格子里填入尽可能大的运量40。同时由于客户B的需求已经满足，故将B₁列用虚线划去，A₁的发货量相应地改为30，见表7-10。

表7-10 （单位：t）

（2）在表7-10的基础上重复上述过程，可得初始方案，见表7-11。

表7-11 （单位：t）

注：表7-11中由A₂运往B₂的运量为0，表示不需A₂运送货物给B₂，因为客户B₂的需求已经满足。

初始方案对应的总运费为

40×3+30×6+0×3+70×3+10×4+50×2=650元

第二步：用位势法检验初始方案是否为最优。

（1）首先构造位势表 把运价表中对应于表7-11中有调运量的运价圈起来，同时在右边添加一列，下面添加一行，并在所添加的行、列的格子中填入一些数字，这些数字使圈起来的任何一个运价数正好等于它所在行及所在列中新填入的数字之和，详见表7-12。

表7-12（单位：t）

(www.daowen.com)

（2）求检验数 在初始方案中位于A_i行和B_j列的格子对应的检验数记为λ_ij，则：

λ_ij=A_i行的位势数+B_j列的位势数-C_ij

其中C_ij为由A_i运往B_j的运价。

当所有λ_ij≤0时，对应的方案为最优方案。由此可得：λ₁₁=0+3-3=0；λ₁₂=0+6-6=0；λ₁₃=0+6-2=4＞0；λ₁₄=0+7-4=3＞0；等等。

由于λ₁₃=0+6-2=4＞0，说明初始方案不是最优方案，由此转入下一步。

第三步：利用“闭回路法”调整初始方案。

（1）在表7-9中做出以与λ₁₃对应的空格为起点的闭回路。见表7-13，并求得调整量ε。ε等于该闭回路上由空格算起奇数次拐角点上的最小运量。

ε=min{30，70}=30

表7-13 （单位：t）

（2）在该闭回路上，偶数次拐角点上的运量都加上调整量ε，奇数次拐角点上的运量都减去调整量ε，不在该闭回路拐角点上的其他各运量都不变。调整后的新的方案，如表7-14。

表7-14 （单位：t）

第四步：依照上述方法对方案进行检验、调整，直到所有的检验数都为正，得到最优方案为止。最优方案见表7-15。

表7-15 （单位：t）

最优方案所对应的总运费为

70×2+30×3+0×3+50×4+40×1+10×2=490元。