储运仓库（或货运车站）要把各个客户所需的零担货物组成整车，通过铁路运往各地。整装零担车内装有多个客户的货物，要分别在一站或多站卸货。一些外观相近的货物，例如金属管材、线材，很容易混淆，到站卸货容易出现错卸现象。有时因为捆扎包装不牢而散捆破包，更容易造成差错。这种差错将给客户和仓库造成经济损失，也给铁路运输带来混乱。为了减少或避免这种差错，可以把外观相近、容易混淆的货物分开装载，尽量不要配装在一个车厢内。为了解决这个问题，可以把货物进行分类，按品种、形状、颜色和规格把货物分为若干类，分别称为1类，2类，…，m类。设共有N件（捆）待运货物，其中1类货物有N₁件（捆），它们的质量分别为G₁₁，G₁₂，…，G_1N1；2类货物有N₂件（捆），它们的质量分别为G₂₁，G₂₂，…，G_2N2；依此类推。即

设

品种混装要求在同一货车内每类货物至多装入一件（捆），同一客户的多件（捆）同类货物可以记作1件（捆）。品种混装问题可以表示为

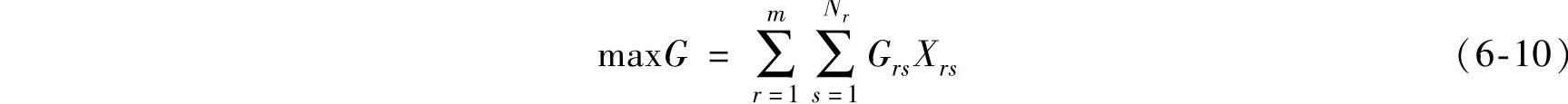
约束条件为

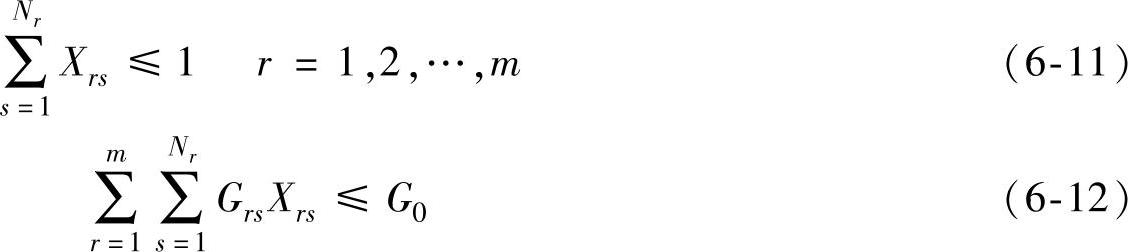
其中G₀表示货车的载质量上限。

上述问题是一个整数线型规划问题，可以用单纯形法和COMORY方法求解。

下面介绍另一种求解方法。图6-1表示8件货物分为4类，在图中同一列的方框表示同一类货物。方框内的数字（符号）表示货物质量。上述品种混装问题就是在网络中自右向左寻找一条路线，使路线所经过的方框中的质量之和达到极大，但又不超过货车的载质量的上限G₀。

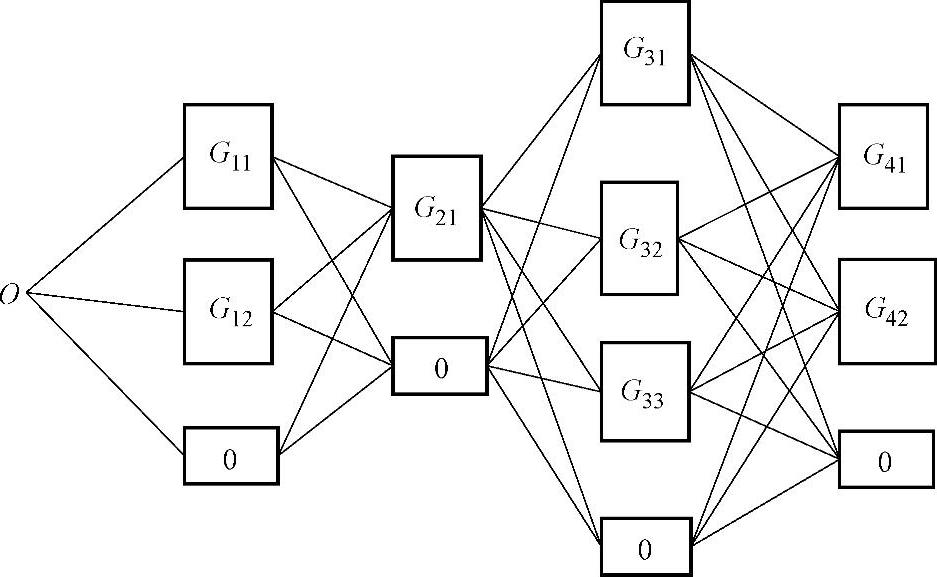
图6-1 混装问题的网络表示图

这种问题可以用穷举法求解，即比较各条路线的载质量从而求出不超过G₀的最大装载量的路线。四类货物也可以看作四个阶段，上述问题化为动态规划问题求解。

例：货车额定载质量G₀=50；第一类货物2件，G₁₁=20，G₁₂=11；第二类货物1件，G₂₁=13；第三类货物3件，G₃₁=6，G₃₂=11，G₃₃=8；第四类货物2件，G₄₁=19，G₄₂=17。计算过程见表6-9至表6-12。(www.daowen.com)

解：

表6-9 第四阶段计算表

表6-10 第三阶段计算表

表6-11 第二阶段计算表

表6-12 第一阶段计算表

寻求最优解次序与计算顺序相反。要使装载量达到极大，则对应的余量应当最小。

在第一阶段计算表6-12中，余量W-G₁的最小值为零，G₁=20对应的W值为20；第一阶段W值对应于第二阶段计算表6-11中的余项W-G₂，对应余项W-G₂=20的有两项，它们所对应的W值分别为20和33；查第三阶段计算表6-10，余项W-G₃为20（或对应G₂=0）时，G₃₃=11，W=31，余项W-G₃为33（或对应G₂=13）时，G₃=0，W=33；再查第四阶段计算表6-9，余项W-G₄为31（或对应G₃=11）时，G₄=19，余项W-G₄为33（或对应G₃=0）时，G₄=17。寻找过程可以表述为：

G₁=20→G₂=0→G₃=11→G₄=19

G₁=20→G₂=13→G₃=0→G₄=17

这就是所求的两组最优解。每组装载量都是50，达到满载，充分地利用了货车的装载能力。