设车辆的载质量上限为G，可用于运送n种不同的货物，货物的质量分别为W₁，W₂，…，W_n。每种货物分别对应一个价值系数，用P₁，P₂，…，P_n表示（可用货物价值、运费或质量等指标表示）。设X_k表示第k种货物的装入数量，则装货问题可表示为

约束条件为

可以用动态规划思想求解上述问题，即把每装入一件货物作为一个阶段，把装货问题转化为动态规划问题。动态规划问题求解过程是从最后一个阶段开始由后向前推进。由于装入货物的先后次序不影响最优解，所以求解过程可从第一阶段开始，由前向后逐步进行。具体步骤为：

第一步，装入第一种货物X₁件，其最大价值为

其中，0＜X₁＜[G/W₁]，方括号表示取整数。

第二步，装入第二种货物X₂件，其最大价值为

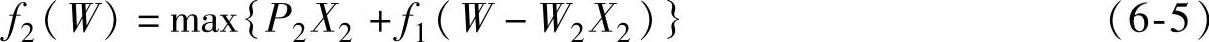
其中，0＜X₂＜[G/W₂]。

第三步，装入第三种货物X₃件，其最大价值为

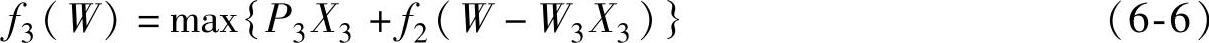
其中，0＜X₃＜[G/W₃]。

……

第n步，装入第n种货物X_n件，其最大价值为

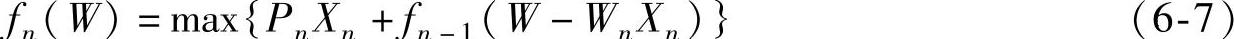
其中，0＜X_n＜[G/W_n]。

例：载质量为8t的载货汽车，运输四种机电产品，其质量分别为3t、3t、4t、5t，见表6-4，试问如何配装才能充分利用货车的运载能力？

表6-4 四种货物的质量和价值系数

注：本例中的价值系数即货物质量。(www.daowen.com)

解：按上述方法，分成四个阶段进行求解，计算结果列成四个表格，见表6-5至表6-8。

表6-5 第一阶段计算表

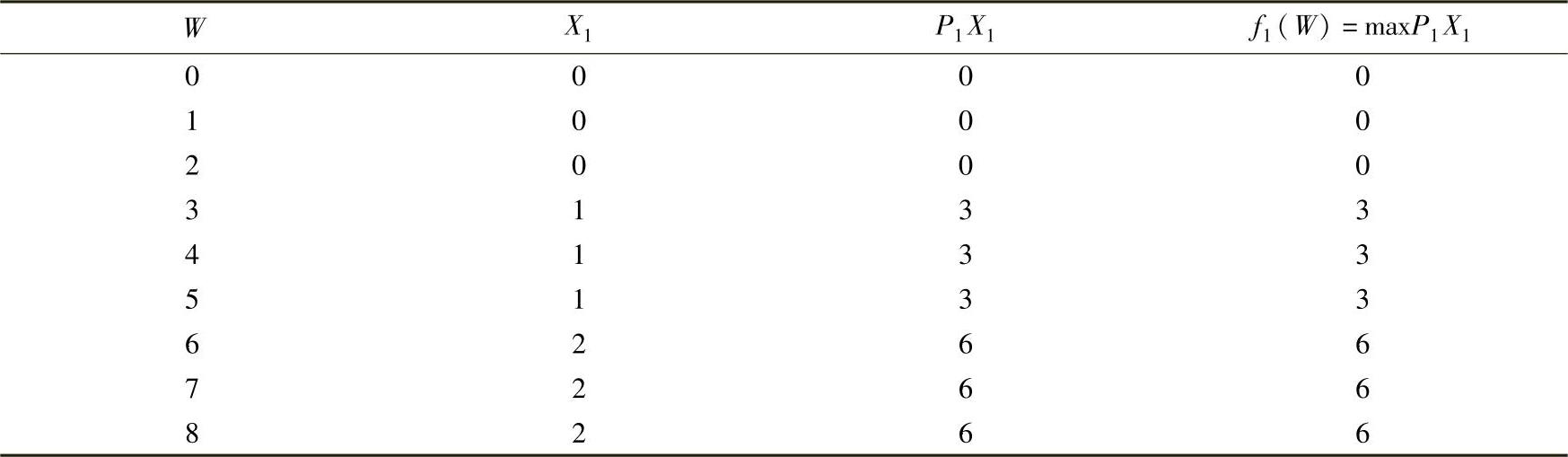
表6-6 第二阶段计算表

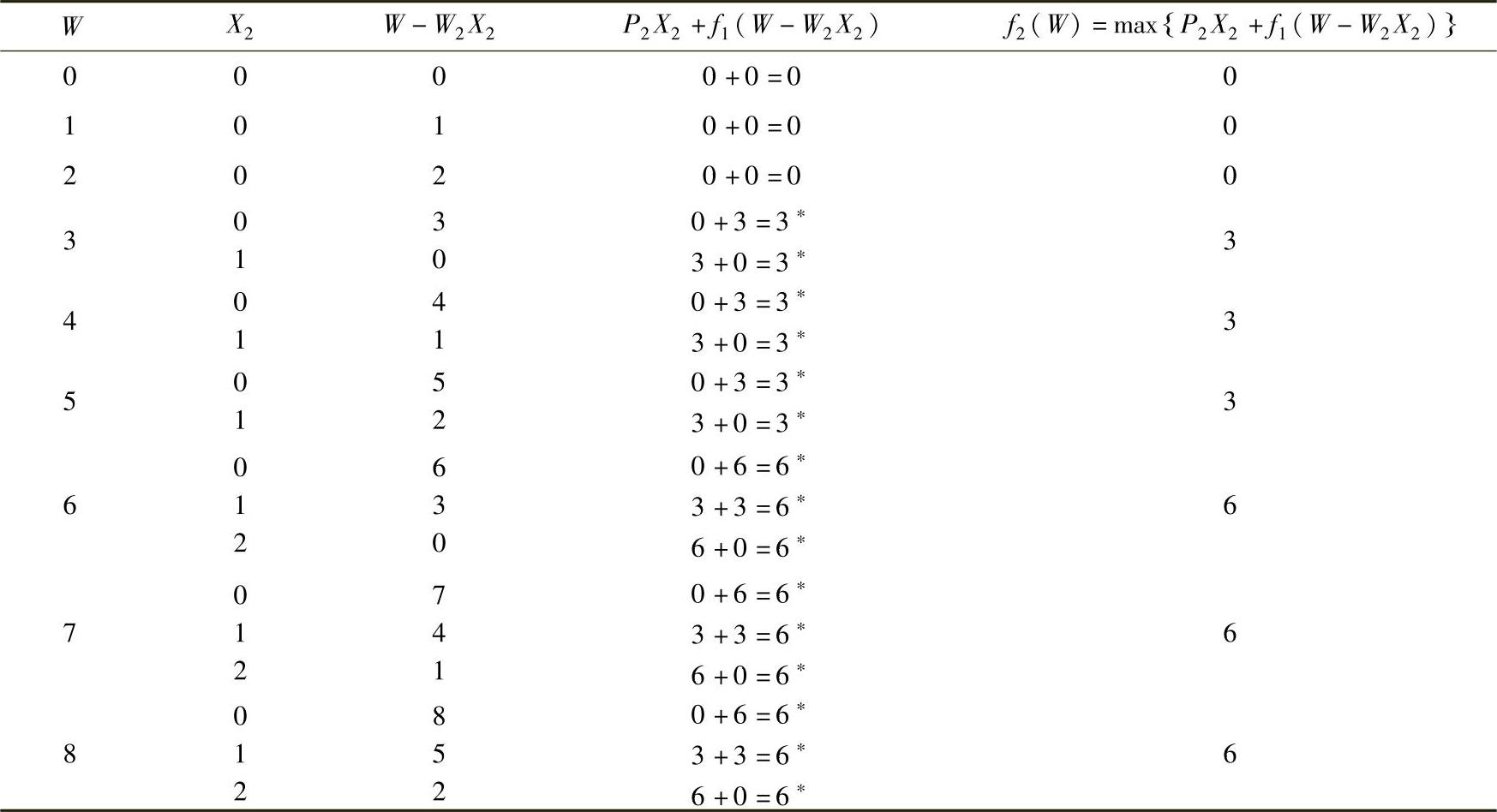
表6-7 第三阶段计算表

表6-8 第四阶段计算表

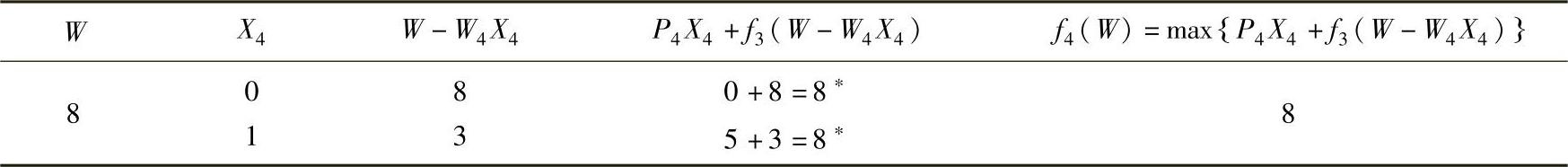
寻找最优解方案的次序与计算顺序相反，由第四阶段到第一阶段进行。

在第四阶段计算表6-8中，价值（本例为载质量）最大值f₄（W）=8t，对应两组数据，其中，一组中X₄=0，另一组中X₄=1。

当X₄=1时，即第四种物品装入1件。表6-8中第3列数字表示其余种类货物的载质量。当X₄=1时，其他三种货物装载质量为3t；按相反方向，在第三阶段计算表6-7中，查W=3t时得装载质量最大值f₃（W）=3t对应X₃=0，查表6-7中第3列数字，当W=3t，X₃=0时，其余两类货物装入质量为3t；在第二阶段计算表6-6中，查W=3t，f₂（W）=3t，对应两组数据：X₂=0或X₂=1，其余量为3t或0t，即其他（第一种）货物装入量为3t或0t；再查第一阶段计算表6-5，当W=3t时，X₁=1；当W=0t时，X₁=0。

因此得到两组最优解：

X₁=1，X₂=0，X₃=0，X₄=1

X₁=0，X₂=1，X₃=0，X₄=1

装载质量为f（X）=1×3+1×5=8t

当X₄=0，则余项W-W₄X₄=8t；在第三阶段计算表3-6中，查W=8t一栏，f₃（W）=8t对应X₃=2，因此得到第3组最优解。

③X₁=0，X₂=0，X₃=2，X₄=0

装载质量为f（X）=2×4=8t

这三组解，都使装载质量达到汽车的最大载质量。