6.2.1.1　DEA模型

Farrel（1957）最早提出了数据包络分析DEA（Data Envelopment Analysis）模型。美国运筹学家A.Charnes、E.Rhode和W.W.Cooper在1978年凭借“相对效率”作为理论基础，对模型进行了不同的改进，用于评价同种类别的具有多输入和多输出的决策单元（DMU）的相对效率与效益。此方式通过运用线性规划建立高效的凸性生产前沿面，并通过和此前的情况进行对比来判断其优劣状况。财政支持战略性新兴产业发展的投入与产出系统包含了对应的多个输入与输出，输入部分不仅仅包括人、财等可以计量运算的有形因素，同时也可以是政策方面的无形内容；而从输出角度来说可以是专利成果，也可以是其所做出的贡献。DEA模型之中有两个重要的大类分别是投入和产出导向性，前者指的是在产出确定的情况下，如何使投入最小化；后者是指在投入一定时，如何使产出最大化。因此，数据包络分析包括两个基本假设：

假设一：如果不增加对资源的投入或减少其他产出项的产出，则某产出项的产出是无法被增加的。

假设二：如果不减少产量或增加对其他投入项资源的投入，则投入是无法被减少的。

1978年A.Chames等人提出了第一个DEA模型——CCR模型，该模型是基于对要素规模报酬不变的假设提出的，基于生产有效性的角度分析，该模型是用来评估“技术有效”和“规模有效”的具有多输入多输出的决策单元。W.W.Cooper（1984）^[2]等假设要素规模报酬是可变量，通过对规模报酬的调整，从而创新出一个DEA的基本模型——BCC模型。对研究财政支持战略性新兴产业发展的效率而言，主要在于如何以最低的财政投入，促进战略性新兴产业产值和规模效益的增长，因此，本章采用投入导向的DEA模型评价财政支持战略性新兴产业发展的效率，具有独特的优势。

不同于传统的计量方法，DEA模型有许多优点：不用预先求出生产函数；不用预先确定指标的权重；不会受指标量纲不同的影响；剔除了非DEA有效的决策单元后，可以得到更准确的评估；通过对比DEA的有效决策单元，可以得出对于经营管理有用的信息^[3]。

在DEA模型中，决策单元要满足“自由度”的要求，即决策单元DMU必须足够多，对于决策单元的个数D与投入指标数M及产出指标数N之间应满足关系：2（M+N）≤D，否则就会降低评估结果的可信度。所以，在DEA模型中，不能选择太多的投入或产出变量，合并相关性较强的变量，减少研究问题的维度，提高分析的准确性。

6.2.1.2　CCR模型

CCR模型通过Charnes-Cooper变换，可以改编成一个等值的线性规划。依照相关的对偶理论，其还可以变为对应的对偶规划，其所涵盖的经济意义为生产可能集与生产前沿面相的呼应。其中生产可能集是生产可能性边界的集合，反映了特定的经济特性。在对该决策单元DEA有效与否的分析过程之中，实际上也就是考虑此单元有没有处在生产性前沿面上。而生产性前沿面，指的就是决策单元的输入和输出数据的包络面的有效前沿。比方说将最小输入以及最大输出为目的，那么对应的前沿面即为，通过生产可能集作为约束条件的相应线性多目标规划的帕累托最优面。

假设生产可能集满足锥性公理，这就是说在CCR模型中的DEA有效，既为“技术有效”，也满足“规模有效”。前者指的是在输出确定的情况下输入最小，也可以使在输入确定的情况之下输出最大。而后者指的是规模收益没有改变，投入则表现为最佳情况。当投入增加时，产出量以低于投入增加的幅度增长，出现规模收益递减。当投入增加时，产出量以高于投入增加的幅度增长，出现规模收益递增。

假设样本数为D（D是决策集，1≤j≤D），所有的D个样本都可以进行比较。对于所有的样本而言都分别具备M和N种的投入与产出类型。DEA对决策单元的效率进行测量的方法就是最大化加权平均产出与加权平均投入，以第j0个决策单元的效率作为目标，约束所有决策单元的效率，构造CCR模型为：

u≥0，v≥0

其中xi=（x1j，x2j，…，xmj）T，yj=（y1j，y2j，…，ynj）T，j=1，…，D；

v=(v1，v2，…，vm)T，u=(u1，u2，…，un)T。

（6.1）是一个分式规划，由Charnes-Cooper变换，并令(www.daowen.com)

得线性规划模型（6.2）：

线性规划的最优解即表明决策单元j0是有效的，从模型（6.2）可以看出，决策单元j0的有效性是相对的。为了分析线性规划（6.2）的经济含义，可以对其进行对偶变换，即：

λj≥0，j=1，…，D

θ没有约束。

加入松弛变量s+和冗余变量s-，同时变换（6.3）中的不等式约束为等式约束，得：

θ没有约束，s+≥0，s-≤0。

线性规划（6.4）也为（6.2）的对偶规划。若线性规划（6.2）和（6.4）的可行解都存在最优值。如果线性规划（6.2）的最优解，则决策单元DMUj0是弱DEA有效的。如果线性规划（6.2）的解中有w*＞0，μ*＞0，且最优解，则决策单元DMUj0是DEA有效的。如果线性规划（6.2）的最优解，则决策单元DMUj0是无效的，此时决策单元存在投入冗余或产出不足，s-*为xj0对应投入的冗余量，s+*为yj0对应产出的不足量。

6.2.1.3　BCC模型

BCC模型，是对决策单元之间的相对技术有效进行评估，其生产可能集T是一个多面凸集，包含了生产可能集的凸性、无效性和最小性。BCC模型的线性规划为：

线性规划（6.5）带有非阿基米德无穷小参数的对偶规划为：

若线性规划（6.6）的最优解值λ*，θ*，s+*，s-*满足θ*=1，且s+*=s-*=0时，决策单元DMUj0技术有效，否则为技术无效。之所以BCC模型可以对比决策单元DMU之间的相对技术有效，是因为其比CCR模型多一个约束条件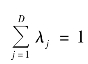。在BCC模型中，其收益分为三种：

如果θ*=1，则规模收益恒定；

如果θ*＜1，且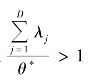，则规模收益递减；

如果θ*＞1，且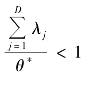，则规模收益递增。