（1）幅域分析法　幅域分析方法是一种早期信号特征分析方法，通过计算信号幅值域诊断参数，来判断齿轮是否处于正常工作状态。常用无量纲幅值域诊断参数作为诊断标准，如波形指标、峰值指标、脉冲指标、裕度指标和峭度指标等，这些诊断参数分别适用于不同的情况，没有绝对优劣之分^[8]。

1）峰值X_P。峰值是振动物体（或质点）在振动过程中偏离平衡位置的最大距离。峰值对早期故障的敏感性比较高，特别是初期阶段齿轮齿面剥落，非常容易由峰值的变化检测出来。另外，对于转速较低（如300r/min以下）的情况，也常采用峰值进行诊断。峰值X_P的公式为

2）均值X。方均值反映了信号下x（t）相对于零值的波动情况，表示信号的平均能量。均值用于诊断的效果与峰值基本一样，其优点是较峰值稳定，但一般用于转速较高的情况（如300r/min以上）。均值X的公式为

3）方均根值X_rms。方均根值是对时间平均的，因而它适用于像磨损之类的振幅值随时间缓慢变化的故障诊断。用方均根值度量振动量级的优点在于：方均根既考虑到了振动时间变化的经历过程（峰值与时间历程无关），又表示了机械振动能量的大小。方均根值X_rms的公式为

4）裕度指标CL_f。裕度指标定义为峰值与方根幅值之比。裕度指标是反映信号冲击程度的一个指标，对齿轮和轴承的冲击故障较为敏感，特别是故障早期时，它有明显的增加；但上升到一定程度后，随着故障的逐渐发展，反而会下降，表明它们对早期故障有较高的敏感性，但稳定性不好。裕度指标CL_f的公式为

5）峭度指标K_v。峭度指标定义为峭度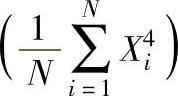与方均根值的四次幂之比。峭度指标是不够敏感的低阶矩与较敏感的高阶矩之间的一个折中特征量，是反映偏离正态分布程度的一个指标，对信号中的冲击成分特别敏感。当设备状态正常时，振动幅值呈正态分布，峭度指标值为3，过高的峭度指标通常反映了局部缺陷，而总体缺陷和分布缺陷通常使概率密度分布趋于平缓，因此使峭度指标降低，即

以上这些时域特征值，在减速器发生故障时可以反映故障的发生，有时可以反映故障的程度，并作为粗略判断的依据。

（2）频域分析法　频谱分析是在频域中对原信号分布情况的描述，是机械故障诊断中应用最广泛的信号处理方法之一，包括以快速傅里叶变换为核心的经典傅里叶频谱分析和适用于非对称、非线性系统的双谱分析方法等。经典傅里叶分析是一种纯频率的分析方法，适用线性高斯稳态信号，反映的是整个信号全部时间段的整体频率特征。无论故障诊断技术如何发展，这种频谱分析技术仍是基础，在实际应用中不可或缺^[9]。幅值谱分析是直接对采样所得的时域信号进行傅里叶变换，求得关于该时域信号的频率构成信息，其数学表达式为

式中，x（t）为时域信号。

对于周期信号，经过傅里叶变换后得到的幅值谱是离散谱，即构成信号的频率成分是基波及其各次谐波分量。而对于非周期信号，其幅值谱是连续谱，即信号连续分布在一定的频率范围内。幅值谱是在频域中对信号能量分布情况的描述，它表示单位频带内信号幅值随频率的变化情况，也就是说反映信号幅值在频域内的分布情况。对于故障信号，其在幅值谱上经常表现为有较大的峰值出现。根据峰值出现时的频率即可判别是否有故障及故障的类型。

图2为齿轮断齿故障的振动信号频谱图，从图中可以看到，啮合频率两侧有明显的边频带产生，即可以确定齿轮出现故障。但是无法找到调制信号的频率，所以不能准确地判断具体是什么故障。需要运用解调方法，并找到调制信号的频率，与特征频率对应就可以找出具体出故障的原因。(www.daowen.com)

图2 齿轮断齿故障的振动信号频谱图

利用时域参数可以快速实现对设备简易诊断，即判断是否存在故障，故常用于对齿轮箱的在线监测。当需要分析故障类型、故障位置及故障严重程度时，就要对齿轮箱的振动信号进行频谱分析。根据频谱图中的频率成分及各有关频率成分的幅值大小进行进一步诊断。

（3）时域相关分析　为了描述随机序列不同时刻状态之间的内在联系及两个随机序列不同时刻状态之间的彼此联系，常应用相关函数。自相关函数描述的是同一信号中不同时刻的相互依赖关系，其定义式为

其离散化计算公式为

相关函数是τ的函数，称之为时延或时差。因此，相关分析又可称之为时延域分析或时差域分析。对测取的振动信号进行相关分析能显著地抑制噪声。

自相关函数具有以下重要特性：

①自相关函数是偶函数；②当τ=0时，自相关函数具有最大值；③周期信号的自相关函数仍然是同频率的周期信号，但不具有原信号的相位信息；④当随机信号的均值为0时，自相关函数将随τ值的增大而很快趋于零。均值不为0时，自相关函数很快趋近于平均值的平方。

由自相关函数的性质可知，在参变量τ=0附近相关函数的值很大，自相关后的剩余噪声多集于此处，而对此自相关函数进行适当时延，将会进一步抑制噪声。因此，自相关函数可以从随机信号中检测出周期信号，具有显著的降噪效果。

利用自相关分析来去除噪声部分、降低信号干扰，从图3a、b对比可以看出。图3a是原始振动信号的时域波形及其幅值谱，图3b是自相关降噪之后的信号及其幅值谱（即原始信号的功率谱）。图3b中的时域波形已经可以看出明显的调制周期性，幅值谱图的噪声干扰也明显降低，达到降噪效果。

图3 自相关降噪前后的频谱图