知识密集型众包任务和接包方的匹配模型建模的过程可以初步化解为三步:第一步,了解匹配双方需求;第二步,根据双方需求设计实现匹配的流程;第三步,探索信息数据化和实现匹配的科学方法。在知识密集型众包任务与接包方的匹配中,任务发包方最迫切的需求是在众多的接包方中找到能承担并出色完成任务的接包者,而接包方最迫切的需求是从平台的众多任务中找到自己能承担且酬金水平能够接受的任务,两者在人工匹配需求中的最大阻力是信息过载。由于从接包方的需求出发探索两者的匹配不仅涉及接包方的主观动机,数据难以量化,且数据量庞大,难度较大。本章将从任务发包方的需求出发,以为发包方选择最优接包者的角度探索知识密集型众包任务与接包方的匹配方法。

在对一个平台上的接包方与任务进行匹配之前,首先需分清平台上的方案众包的模式,国内众包平台的模式主要分为悬赏模式和投招标模式,两者区别很大,如任务难度的区别,预提交成果完成度的区别,反映在匹配设计过程中的区别主要是酬金金额确定方式。悬赏模式往往在发布任务的同时就公布了悬赏金额,而投招标模式的酬金金额一般由接包方在竞标时提出或在中标后与发包方协商提出。金额确定方式不同对匹配指标设计有影响,本章所设计的模型主要针对投招标模式。

任务与接包方匹配的流程如下:发包方在发布任务后吸引感兴趣的接包方参与任务的竞标,根据任务的要求筛选符合基本要求的接包者后,根据接包方在平台上的历史数据和注册信息,量化为候选人的各项指标数据,再通过TOPSIS多指标决策算法得出最优接包方。在使用该算法实现匹配的过程中,需要在平台网站中抓取数据,为接包方设计适合匹配的匹配指标,同时选取合适的权值确定方法确定权值,使用多指标决策算法得出最优解。

6.3.1.1　指标设计原则

匹配指标设计是匹配模型中最核心的部分,决定了将哪些接包方信息纳入匹配指标中,决定着最终匹配结果。匹配指标设计是否合理关系着匹配是否合理、有效、精确。

指标的设计不是简单的堆砌和组合,要求具备合理性、可操作性和系统完整性,具体原则如下:

(1)合理性:指标的合理性是指在设计指标的过程中,应遵照现实情况和需求,围绕最终的评测目的科学选取合适的指标。指标的选取应注意情境依赖,在不同的平台不同的知识密集型任务类型中,选取能对接包方的能力评估起重要作用的指标,且指标概念无歧义、不重合。

(2)可操作性:指标的可操作性指构建指标应是可行的,主要包括构建指标数据容易取得和数据可量化两个方面。所需要的数据应尽量有可方便获取和统计的数据来源,且应尽量避免定性指标,或选取可赋值和测算的定性指标。

(3)系统完整性:指标的系统完整性是指应站在整体的高度设计指标,尽量涵盖接包方评估所需要考量的各个方面,全面地反映任务所需的接包方的能力,且在设计过程中,应有层次有关联地安排指标体系,以使其能有清晰的结构。(www.daowen.com)

在下一节中将着重讲解匹配指标的设计。

6.3.1.2　数据处理

在进行匹配之前须针对平台,寻求可抓取的能反映接包方是否与任务匹配的数据,最基础的包括:接包方在平台上的注册信息,接包方在平台上的历史活动数据。接包方数据应以所参与任务为一组。根据可得到的数据设计指标,并将数据转化为指标数值,为算法更加便易,需将其中的负收益性指标转化为正收益性指标。设预处理后的原始数据有n条,指标有m个,指标矩阵为X。

6.3.1.3　权值确定

在指标设计完成之后,需要根据实际需要对各指标赋权,本章将采取AHP－熵权法,结合主客观赋值,确定指标权重。首先将某任务的接包方指标数据处理为正收益值,构造原始指标矩阵,运用上一章中的熵权法,求出客观指标权值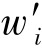;而主观指标的计算则采用AHP层次法来确定,这样就需要人工判断各层次指标之间的相对重要性。若由任务发布者来判断相对重要性,能准确地体现任务对接包方的要求,但在实际情况中,对发包方来说占用了太多时间,且发包方的判断往往受自身经验限制可能造成误判。所以,在实际情况中,可由专家就该领域该模式的匹配来判断指标相对重要性,计算出各层权数,再通过递层赋权可确定主观指标权值;如上章所述,可通过引入加权系数α,根据式(6.13)将两种权值结合起来,得到最终权值wi。

6.3.1.4　算法实现与运算

在获得接包方指标数据和指标权值之后,将原始指标数据X根据式(6.16)归一化处理为标准矩阵Z,再将Z中的标准指标值分别与求得的最终权值相乘,得到加权矩阵Y,其中:

得到Y后就可根据公式(6.17)与(6.18)得到正理想解Z＋和负理想解Z－,继而通过公式(6.19)(6.20)和(6.21)得出各方案与正理想解的相对近似度Ci,Ci最大的候选者就是该匹配模型下的最优接包方。