在多指标决策中,由于每个指标对最终结果的重要程度不同,需要根据每个指标的重要性程度赋予不同的权重。多数学者将确定权重的方法分为主观赋值法和客观赋值法。主观赋值法,即计算权重的原始数据主要由评估者根据主观经验判断得出,包括主观加权法、专家调查法、层次分析法(AHP)、模糊统计法等;客观赋值法,即计算权重的数据由各评测指标在被评测过程中的实际数据得到,如均方差法、主成分分析法、熵值法、代表计算法等^[2]。两类赋值方法各有优缺点,主观赋值法考虑到评测人员的主观感受,但由于受评测人员的个人影响容易产生偏颇;而客观赋值法数据来源于指标数据的统计分析,一定程度上排除了评测人员的主观影响,但也可能由于数据分析模型的不适用或数据误差造成与实际情况不相符的问题。

发包方在为任务挑选接包方时需根据自己的需求对接包方的各方面能力进行评估,而评估的过程往往是复杂模糊的,依靠主观判断无法直接计量,在模拟评估的过程中,就要求指标之间具有层次关系,需要主观赋予指标不同权值来进行算法判断。而层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程具有相似性,即从上而下将不同因素分解为若干层次,比较因素间的重要程度,能很好地模拟主观赋值的过程,适合任务与接包方的匹配模型的主观赋值方法。

另外,在对接包方进行评估时,所获得的评估指标之间有信息量多寡的区别。以猪八戒网为例,对比接包方好评率和总收入这两个指标,接包方的好评率往往集中在90%～100%,而接包方的收入却从零到几百万元不等,在这种情况下,接包方的收入这一指标比好评率这一指标包含更多可区分接包方能力的信息,应给予更多的权重,而熵权法根据信息无序程度确定权值,给予信息熵小的无序程度大的指标更多的权重,因而适合作为为任务与接包方匹配指标客观赋值的一种方法。

本小节将简要介绍这两种比较典型的权重确定方法。

6.2.1.1　层次分析法确定权值

在20世纪70年代初,美国著名运筹学家Satty提出层次分析法(analytical hierarchy process,AHP),是将一个复杂的多方案决策问题作为一个系统,将总目标分解为多准则的若干层次,通过定性指标模糊量化方法算出层次单排序和总排序,以作为多方案优化决策的系统方法,常用来解决综合评价、选择决策方案等问题^[3]。

层次分析法的基本原理是将一个复杂问题分层,一般分为目标层、准则层、方案层等几个层次,最后一层有时也可称为指标层。通过两两比较的方式,比较同层中的两个因素对上一层中某事物的影响的重要性,继而确定该层次中元素的相对重要性,建立判断矩阵。使用数学方法计算将每个层次的判断矩阵归一化处理为各指标的相对重要性权值,进而通过递阶层次计算全部指标对目标的重要程度权数。步骤算法如下。

(1)构造判断矩阵。

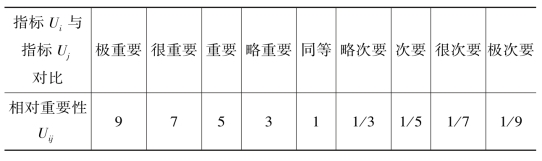
设某一层中的指标为Ui(i＝1,2,...,n),将指标Ui对上一层中的父指标Am的重要性与指标Uj对父指标Am的重要性进行对比,得到相对重要性Uij,比例标度参照Saaty 1-9比率标度法,如表6-1所示。

表6-1　相对重要性比例标度

由此构造判断矩阵如下:

(2)矩阵归一化处理。

将判断矩阵P的各行向量进行几何平均,然后归一化,得到的行向量就是权重向量。算出判断矩阵每一行指标的乘积:

计算乘积的n次方根:

对向量归一化处理,算出指标权重Wi:

(3)一致性检验。

为验证所得的权重是否合理,还需对判断矩阵进行一致性检验。步骤如下:

计算矩阵的最大特征根:

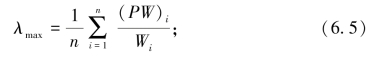
计算判断矩阵的一致性指标:

计算随机一致性比率:

一般来讲,当判断矩阵的一致性比率CR＜0.10时,即认为判断矩阵具有满意的一致性,否则需要调整判断矩阵,以使之具有满意的一致性。R.I.是平均随机一致性指标,可根据阶数在量表中查询,如表6-2所示。(www.daowen.com)

表6-2　平均随机一致性指标R.I.值

6.2.1.2　熵权法确定权值

1948年,Shannon将熵的概念引入信息论中,作为信息的一个度量^[4]。信息是系统有序程度的一个度量,熵是系统无序程度的一个度量,信息的增加意味着熵的减少。当评价对象在某项指标上的值相差较大时,熵值较小,说明该指标提供的有效信息量较大,该指标的权重也应较大;反之,若某项指标的值相差越小,熵值较大,说明该指标提供的信息量较小,该指标的权重也应较小^[5]。当各评价对象在某项指标上的值完全相同时,熵值达到最大,这意味着该指标未向决策提供任何有用的信息,可以考虑从评价指标体系中去除。熵权法是一种客观赋值的方法,可运用多个指标对多个被评价对象进行评价,也可用于剔除指标体系中对评价结果贡献不大的指标。

计算熵权的步骤如下:

(1)原始数据矩阵标准化。

设有m个指标和n个评价对象,可建立原始数据矩阵为:

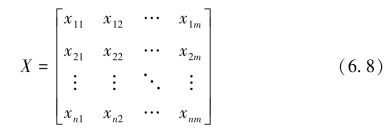
矩阵标准化可得:R＝(rij)n×m。其中rij为第j个评价对象在第i个评价指标上的标准值,对正收益性指标而言:

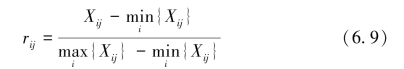
对负收益性指标而言:

(2)定义熵和熵权。

第j个指标的熵可定义为:

其中,当fij＝0时,令fijln fij＝0;第j个熵权可定义为:

其中。

熵权并不是表示决策评估问题中评价指标实际意义上的重要性系数,而是在给定评价对象集后各种评价指标值确定的情况下,各指标在竞争意义上的相对激烈程度。从信息角度考虑,它代表该评价指标在该问题中提供有效信息量的多寡程度,作为一种客观综合评价方法,它主要是根据各指标传递给决策者的信息量大小来确定其权数^[6]。

6.2.1.3　AHP-熵权法

将AHP与熵权法结合起来是为多指标复杂系统分配指标权重的更优办法,一方面避免仅利用AHP法进行价值评价时主观性太强的弱点,同时弥补熵权法缺乏专家经验知识的不足,使评价模型在追求客观实际的同时结合各项目的独特性和专家的经验判断。学者们提出了两种结合方法:

(1)引入加权系数α。

在这里我们引入加权系数α,以综合层次分析法和熵权法所得到的权值^[7],应用如下公式来确定最后的指标权值Wi:

其中,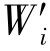表示由层次分析法得出的权值,而表示由熵权法得出的权值。当加权系数α的值越大时,主观评论对权值确定的影响越大;反之,客观分析的影响越大。

(2)分层次使用两种方法确定最后的权值。

有学者认为可以利用AHP的层次结构,在准则层对目标层的权重分析中采用层次分析法,在指标层对准则层的权重确定中采取熵权法赋值,最后递阶计算各个指标对目标层的权重^[8]。