按照上一节中提出的分解模型步骤对此复杂任务Q进行分解:

步骤一:由于此复杂任务具有明显的时序关系和结构关系。因此按时序与结构相结合的方式对Q进行初步分解,可以得到任务初步分解集合S1。S1集合元素如图5-5“任务初步分解集合S1” 所示。S1包含5项子任务,分别是子任务A,包括a、b、h;子任务B,包括h、k、n、o;子任务C,包括d、e、j、l、q;子任务D,包括f、h、g、c、i、m、l;子任务E,包括l、j、p、r、s、t。

图5-5　任务初步分解集合S1

步骤二:对这5项子任务进行任务类型分析。发现以上子任务在信息交互上都存在一定依赖,因此进入步骤三进行进一步分解。

步骤三:对任务粒度进行合理性控制。在此,根据经验将项目粒度阈值设为0.03。根据分解模型中的算法,可以得到活动约束结构为:

根据式(5.9),集合中各任务粒度系数计算结果如表5-1所示:

表5-1　任务粒度相关系数

根据任务粒度式(5.10)计算可得:

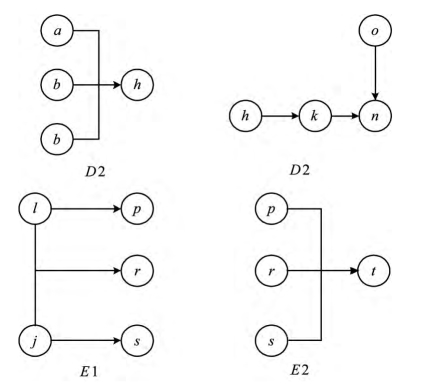
由于St结果为0.0347,大于任务粒度阈值范围,因此对继续进行分解。因为子任务D和E的系数乘积相较于其他任务最大,因此对D进行继续分解为D1和D2,E继续分解为E1和E2,如图5-6所示。

(www.daowen.com)

图5-6　对D、E进一步分解

重复之前的步骤,得出新的集合的粒度为:

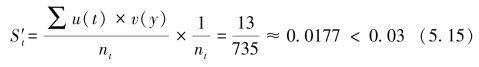
此结果在任务粒度阈值范围之内,进入步骤四。

步骤四:对任务耦合度的合理性控制。根据20个子任务组成的复杂任务分解经验,设定任务耦合度阈值为0.4。根据式(5.11)、式(5.12),任务信息相关矩阵如下表所示:

表5-2　设计结构矩阵

续表

根据式(5.13)可得,S2任务耦合度为:

计算可得,该集合超出了任务耦合度阈值,因此需要将信息交互量多的任务进行合并。由上表可知,D1与E1之间的信息交流较为频繁,因此将其进行合并为DE1。根据以上方法重新计算任务耦合度。结果为:

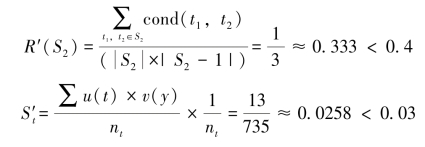
因此S2为任务分解的最优解。重新编号后有子任务,如图5-7“优化分解后的子任务”所示。