进行假设检验之前，对概念模型的测量模型进行检验是非常必要的一项工作。模型适配度的检验一般包含违反估计检验、整体模型适配度检验和内部结构适配度检验三个部分（吴明隆，2008）。

1.违反估计检验

在使用CFA 估计模型之前，要先检查参数估计值的合理性，检验是否存在以下违规估计的现象：①有无负的误差变异数存在；②标准化系数是否在0.50～0.95，是否超过或太接近于1；③有无太大的标准化误差。

2.整体模型适配度检验

测量模型整体适配度的评价指标，一般可分为3 类：第一类是绝对适配度指标（absolute fit measures），它用于决定理论的整体模型能够预测观测共变数或相关矩阵的程度，如RMSEA、GFI、AGFI、SRMR 等；第二类是相对性适配指标（comparative fit index），它是将理论模型和基准模型比较得到的统计量，如NFI、NNFI、IFI、RFI、CFI 等；第三类是简约适配指标（parsimonious fit measures），它用于呈现需要达成某一特殊水准的模型适配的估计系数的数目，如PNFI、PGFI、AIC、CAIC 等。

对于评价模型拟合度的指标，不同学者的看法也不相同。总体来说，一个理想的拟合指数，应包括以下3 个方面特征：①与样本容量N 无关，即拟合指数不受样本容量的系统影响；②惩罚复杂模型，即拟合指数要根据模型参数多寡而做调整，惩罚参数多的模型；③对误设模型敏感，即如果所拟合的指数不真（参数过多或过少），拟合指数能反映拟合不好。要保证基于拟合效果良好的模型来对理论假设进行验证，至少达到多于一个参数标准是必需的。

Hu 和Bentler（1998，1999）建议在结构方程模型中报告χ2、d f、RMSEA、TLI（NNFI）、CFI、IFI 和SRMR 的值。Kline（2004）认为结构方程模型中至少应报告χ2、RMSEA、CFI、SRMR 的值。温忠麟、侯杰泰和Marsh（2004），侯杰泰、温忠麟和成子娟（2004）认为，在结构方程模型中报告χ2/d f、TLI（NNFI）、CFI、RMSEA 的值即可，并且他们认为直接用χ2检验推断一个模型是否与数据拟合并不妥当，因为χ2的大小与样本容量N 有关，当N 很小时，χ2往往很小，使得与真实模型相距很远的错误模型也给人拟合得好的印象；而当N 很大时，χ2则很大，一个模型只要与真实的模型有很小的差距，就可能被认为拟合不好，χ2及其自由度d f 主要用于比较多个模型。陈晓萍、徐淑英和樊景立（2008）认为应该报告χ2/d f、TLI（NNFI）、CFI、RMSEA 和SRMR 的值。刘二丽（2007）认为，除了绝对和相对适配指标外，还应报告简约适配指标PNFI 的值。由于RMR、GFI、AGFI、NFI 和RFI 受样本容量的系统影响较大，学者们并不推荐使用。在参考上述研究的基础上，本研究用于评价模型拟合度的指标及其适配标准见表6-29。

表6-29　SEM 整体模式适配度的评价指标及其评价标准

（1）绝对适配度指标

绝对适配度指标包括χ2/d f（卡方自由度比）、RMSEA（近似误差均方根）、SRMR（标准化残差均方根）。χ2/d f 表示假设模式的共变数矩阵与观察资料间的适配程度。卡方自由度比值越大，表示模式的适配度越差。当χ2/d f 小于1 时，表示过度适配；当χ2/d f 的值介于1～3 之间时，表示模式的适配良好；当χ2/d f的值介于3～5 之间时，表示模式可以接受；当χ2/df 的值大于5 时，表示模式适配度不佳。本研究以χ2/d f 的值不超过5 作为标准。RMSEA 的值越小，表示模式的适配度越好。一般而言，其数值在0.08～0.1 之间表示模式尚可；其数值在0.05～0.08 之间表示模式适配良好；其数值小于0.05 时，表示模式适配度非常良好（Browne 和Cudeck，1992）。本研究以RMSEA 不超过0.1 作为标准。SRMR最早是由Hu 和Bentler 于1995 年提出的适配指标，SRMR 的值越小，表示模式的适配越好，一般而言，其数值小于0.05 时，表示模式适配非常良好（Hu 和Bentler，1995），其数值在0.05～0.08 之间表示模式适配良好（Hu 和Bentler，1998），其数值在0.08～0.1 之间表示模式尚可接受（Schermelleh-Engel K、Moosbrugger 和Müller，2003；Kline，2004），本研究以SRMR 不超过0.1 作为标准。

（2）相对适配度指标

相对适配度指标包括CFI（比较适配指数）、NNFI（非规范适配指数）、IFI（增值适配指数）。当CFI、NNFI、IFI 的值大于0.9 时，表示模型的拟合效果较好；当CFI、TLI、IFI 在0.8～0.9 之间时，表示该模型的拟合效度是可以接受的。

（3）简约适配度指标

简约适配度指标包括PNFI（简效规范适配指数）。PNFI 把自由度的数量纳入预期获得的适配程度的考量中，一般以PNFI 的值大于0.5 作为模式适配度通过与否的标准。即PNFI 的值在0.5 以上，表示假设理论模式是可以接受的。

3.内部结构适配度检验

内部结构适配度主要从建构效度与信度两个方面进行检验。建构效度是指量表能够测量出其所要测量的理论或概念的程度。建构信度或称为组合信度（Construct Reliability，CR），是指一组潜在构念指标的一致性程度，即所有测量指标分享该因素构念的程度。(www.daowen.com)

建构效度一般包括聚合效度（Convergent Validity）和区别效度（Discriminant Validity）两种形式。聚合效度（Convergent Validity）是指测量相同潜在特质的题项或测验会落在同个因素构面上，并且题项或测验间所得到的测量值之间具有高度相关性（吴明隆，2008）。对于聚合效度的检验，可以根据观测变量的标准化因子负荷及其显著性来判断，如果同一理论概念的不同观测变量的因子负荷值均显著大于0.5，则说明测量量表具有较好的聚合效度（Fornell 和Larcker，1981；Chau，1997）。聚合效度还可以用平均变异数抽取量（Average Variance Extracted，AVE）来测量，AVE 的计算公式为：

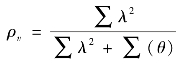
其中，

ρv——平均变异数抽取量；

λ——观测变量在潜变量上的标准化参数；

θ——观测变量的测量误差。

AVE 评价了潜变量相对于测量误差来说所解释的方差总量。如果所提取的潜变量的平均变异量大于或等于0.5，则表示潜变量的测量有足够的聚合效度（Bagozzi 和Yi，1988）。

区别效度（discriminant validity）是指构面所代表的潜在特质与其他构面所代表的潜在特质间有低度相关或有显著的差异存在。即当量表与不同概念的测量工具相关程度很低时，说明该量表具有较好的区别效度。对于潜变量之间区别效度的检验，可将两个潜变量的未限制模式（潜变量间的共变关系不加限制，潜变量间的共变参数为自由估计参数）与限制模式（潜变量间的共变关系限制为1，潜变量间的共变参数为固定参数）的卡方值相比较，如果限定模式的卡方值比未限定模式的卡方值大且达到显著水平（P<0.05）时，则表示潜在变量具有较高的区别效度（Bagozzi 和Phillips，1982；Anderson 和Gerbing，1988；Chau，1997）。

潜在变项的建构信度（CR）计算公式如下：

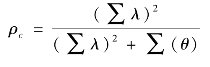
其中，

ρc——建构信度；

λ——观测变量在潜变量上的标准化参数；

θ——观测变量的测量误差。

学者们对建构信度所需要达到的最低标准存在不同的看法。Bagozzi 和Yi（1988）认为建构信度在0.60 以上，就表示潜在变项的建构信度良好。Hair 等（1998）认为建构信度最好在0.70 以上。Raines-Eudy（2000）采用更低标准，认为建构信度只要在0.50 以上即可。Kline（2004）认为建构信度系数在0.90 以上是最佳的，0.80 附近是非常好的，0.70 附近是适中的，0.50 是最低可以接受的值。本研究采用Hair 等（1998）的观点，以0.70 作为建构信度的最低标准。

以下本研究依据Bentler 和Chou（1987）、Sethi 和Carraher（1993）的建议，先将测量模型分为国际代工环境、生产运营战略、国际代工绩效三个子测量模型，分别通过验证性因子分析进行检验，然后再对测量模型的区别效度进行检验。