在寡头市场条件下，厂商的产量和价格的决定相比较于前三种市场结构要复杂得多。这是因为，在前面所分析的市场结构中，厂商在做出价格和产量的决定时，基本上不用考虑其竞争对手的决策。在完全竞争和垄断竞争市场上，由于行业中厂商的数量非常多，从而每个厂商的规模和实力也比较小，因此每个厂商只要根据边际收益等于边际成本的利润最大化原则来进行决策就可以了，而不需要考虑其他厂商的反应；在垄断市场上，由于整个市场只有一个厂商，因此也不需要考虑其他厂商的反应。而在寡头市场中情况就不同了，寡头市场中的厂商数量非常少，每个厂商的规模和实力都相当大，因此每个厂商在进行经济决策时都不得不考虑其他厂商的反应，并根据这些反应来随时调整自己的决策。于是，每个厂商的利润不仅受厂商自己行动本身的影响，还受到行业中其他厂商决策的影响。寡头厂商之间这种相互影响的复杂关系使得他们在进行产量和价格决策时变得复杂。一般地，不知道竞争对手的反应方式，就无法建立寡头厂商的决策模型，或者说，有多少关于竞争对手反应的假定，就有多少寡头厂商的决策模型，就可以得到多少不同的结果。因此，在经济学分析中，还没有一个寡头市场模型，可以对寡头市场的价格和产量的决定得出一般性的理论结论。

寡头厂商之间的关系总体上分为相互勾结和不相互勾结两种情况。所谓相互勾结就是寡头厂商之间通过协议的方式来确定产量和价格。在这种情况下，各个寡头厂商之间实际上已经形成了一个垄断组织，其决策方式类似于垄断市场的情况。而不相互勾结则是指寡头厂商相互独立决策而又同时考虑其他厂商的反映的情况。我们对寡头市场的分析主要是基于不相互勾结的情况。下面以古诺模型为例来说明不相互勾结的寡头厂商是如何进行决策的。

古诺模型由法国经济学家古诺于1838年首先提出。该模型有如下一些基本假定：第一，行业内只有两个厂商A和B，每个厂商生产完全同质的产品，并以追求利润最大化为生产目标；第二，为了分析方便，假定生产成本为零；第三，厂商和市场的需求曲线是线性的，且每个厂商都清楚地知道市场的需求曲线和自己所面临的需求曲线；第四，两个厂商都是在已知对方产量的情况下，各自确定能够给自己带来利润最大化的产量，即每个厂商都是消极地以自己的产量去适应对方已确定的产量。

古诺模型关于产量和价格的决定可以用图5-10来说明。

(www.daowen.com)

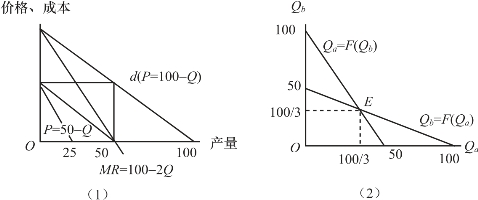
图5-10　古诺模型

在图5-10（1）中，我们假设市场的需求曲线为P＝100－Q，并假定B厂商一开始不生产，此时A厂商面临的需求曲线就是整个市场的需求曲线（P＝100－Q），根据需求曲线方程可以推导出A厂商的总收益函数，即为TR＝100Q－Q2，从而其边际收益函数为MR＝100－2Q。由于假定成本为零，因此边际成本MC＝0。A厂商根据MR＝MC的利润最大化原则确定的产量为50，即A厂商按照市场容量的一半来安排生产以实现自身利润最大化。如果假定B厂商的产量为50，则A厂商此时所面临的需求曲线变为P＝50－Q，利润最大化的产量为25。进一步地，当B厂商的产量为100时，A的市场份额为零，因此其产量也为零。

由以上分析可以知道，厂商A的利润最大化产量水平取决于厂商B的产量，可以认为厂商A的产量就是厂商B的产量的函数，经济学上称这种函数为厂商A对厂商B的反应函数，记为Qa＝F（Qb）。其中Qa，Qb分别表示厂商A和厂商B的产量。同样的道理，我们可以得到厂商B对厂商A的反应函数，记为Qb＝F（Qa）。把两个反应函数所对应的反应曲线描绘到坐标平面上，得到图5-10（2），图中横轴衡量厂商A的产量，纵轴衡量厂商B的产量，两条反应曲线的交点E所对应的产量就是古诺均衡时两厂商产量。在本例中，两厂商的各自生产市场总容量的1/3，即各自生产100/3。

古诺模型是在一系列较为严格的假设条件下得出的结论，虽然不具有普遍的解释意义，但却很好地反映了不相互勾结的而又相互依存的寡头之间的竞争关系。