图4-2　等产量线

（一）等产量线

长期生产理论需要借助等产量线及等成本线（后面介绍）的分析工具。等产量线是指在技术水平不变的条件下，生产同一产量的两种生产要素投入量的各种不同数量的组合点的轨迹。如图4-2所示，在坐标平面上，以横轴表示劳动投入量，纵轴表示资本投入量，则平面中的三条曲线就是等产量线。

等产量线作为长期生产理论的分析工具，具有以下特点：

（1）向右下方倾斜。这一特点表明，在维持原有产量不变的条件下，增加一种要素的投入，同时必须减少另一种要素的投入。

（2）密集分布。即在坐标平面上的等产量线不是一条而是无数条，不同的等产量线代表不同的产量水平，而且离原点越近代表的产量水平越低，离原点越远代表的产量水平越高。如图4-2中所示的三条等产量线，按照离原点的远近，分别代表的产量水平为50、100、150。

（3）任意两条等产量线不相交。因为不同的等产量线代表不同的产量水平，如果两条等产量线相交，则交点处的要素组合所生产的产量既可以由第一条等产量线表示，也可以由第二条等产量线表示，而两条等产量线所代表的产量水平是不同的。

（4）凸向原点。等产量线向右下方倾斜表明了资本和劳动之间的交替关系，在保持产量不变的条件下，增加劳动同时需要减少资本，这表现为劳动对资本的替代。等产量线凸向原点表明，维持原有产量不变时，随着劳动使用量的增加，劳动对资本的替代能力是逐步下降的；反之亦然。

（二）边际技术替代率递减原理

在维持原有产量水平不变的条件下，增加一单位的某种要素投入量时所减少的另一种要素的投入量，称为边际技术替代率。劳动对资本的边际技术替代率公式可写为

MRTSLK＝ΔK/ΔL

式中，ΔK和ΔL分别代表资本和劳动投入量的变化量，即边际技术替代率表现为两要素投入量的变化量之比。显然，资本和劳动的变化方向应该是相反的，因此边际技术替代率的数值应该是负值，但为了分析方便起见，一般都取其绝对值。

在图4-2中，当要素组合由A点变动到B点时，边际技术替代率表现为线段AB的斜率的绝对值。进一步地，当要素投入量的变化趋于无穷小时，A点与B点重合为一点，从而在几何图形上，边际技术替代率表现为等产量线上该点的切线的斜率的绝对值。因此，一般地，边际技术替代率就可以定义为等产量线上点的切线的斜率的绝对值。

此外，边际技术替代率数量上还可以表示为两要素的边际产量之比。这是因为，边际技术替代率的概念是建立在等产量线的基础上的，所以对于任意一条给定的等产量线来说，当用劳动投入去替代资本投入时，在维持产量水平不变的前提下，由增加劳动投入量所带来的产量的增加量和由减少资本投入量所带来的产量的减少量必定是相等的，因此有

|ΔL·MPL|＝|ΔK·MPK|

整理得

ΔK/ΔL＝MPL/MPK

即有

MRTSLK＝ΔK/ΔL＝MPL/MPK

边际技术替代率是递减的，即随着劳动投入量的增加和资本投入量的相应减少，劳动对资本的替代能力是逐步下降的。形成边际技术替代率递减的原因实际上还是前面提到的边际收益递减原理，因为根据边际收益递减原理，随着劳动投入量的增加，其边际产量下降，而相应的，随着资本投入量的减少，其边际产量递增。所以，随着劳动对资本的替代，作为逐渐下降的劳动的边际产量与逐渐上升的资本的边际产量之比的边际技术替代率必然是递减的。边际技术替代率递减的现象通常也称为边际技术替代率递减原理。这一原理通过等产量线凸向原点的特点体现出来。

（三）等成本线

等成本线是分析长期生产理论的另一个分析工具。它是指，在生产要素价格和投入总额一定的条件下，生产者可以购买到的两种生产要素的各种不同数量的组合的轨迹，见图4-3。

在图4-3中，C代表既定成本即投入总额，ω代表劳动的价格，r代表资本的价格。横轴上的点C/ω表示既定的全部成本都购买劳动时的数量，纵轴上的点C/r表示既定的全部成本都购买资本时的数量，连接这两点的线段就是等成本线。它表示既定的全部成本所能购买到的劳动和资本的各种不同数量的组合。等成本线以内区域中的任何一点，如A点，表示既定的成本购买了该点的劳动和资本的组合以后还有剩余；等成本线以外区域中的各点，如B点，表示既定成本购买该点的劳动和资本的组合是不够的；而在等成本线上的各点则表示既定成本购买该点的劳动和资本的组合是刚刚好的。

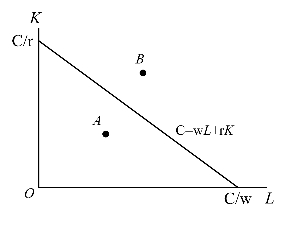
图4-3　等成本线

等成本线的方程可表示为

C＝ω·L＋r·K

式中，C、ω、r都是常数，给定C、ω、r的值，即确定了一条等成本线。由图4-3容易知道，等成本线在坐标平面上的纵截距与横截距之比等于等成本线的斜率的绝对值，从而可知，等成本线的斜率的绝对值等于要素的价格比，即有

由图4-3还容易知道，当C、ω、r的值，即成本或生产要素的价格发生变化时，等成本线将发生变化。关于等成本线的变动可以参照上一章消费者行为理论中预算线的变动来分析，这里不再赘述。(www.daowen.com)

（四）最优要素组合

把等产量线和等成本线放在同一个坐标平面上，就可以确定两种要素的最优组合，在这一组合下，生产者实现了既定成本下的产量最大化或既定产量下的成本最小化，如图4-4所示。

图4-4　最优要素投入组合（一）

在图4-4中，既定的等成本线和密集分布的无数条等产量线有三种关系，即相交、相切和相离。图中的Q1、Q2和Q3与既定等成本线之间就呈现以上三种关系。其中，Q2与等成本线相切于E点，E点即为生产者均衡点，该点对应的劳动和资本的数量就是劳动和资本的最优组合，等产量线Q2所代表的产量水平就是既定成本下的最大产量。

为什么E点是生产要素的最优投入组合呢？这是因为，在图4-4中，等产量线Q3代表的产量水平高于等产量线Q2，但既定的等成本线与Q3既不相交也不相切。这表明，在既定的成本条件下Q3的产量是无法实现的。再看等产量线Q1，它与既定等成本线相交于A、B两点，这表明，Q1是既定成本可以达到的产量，但用同样的成本却可以生产出更多的产量Q2。因此，如果生产者一开始在A点或B点生产，为了在既定成本条件下实现产量最大化，其一定会沿着等成本线把生产点调整到E点生产，以实现更大的产量Q2。等产量线Q2与既定等成本线相切表明，产量Q2是既定成本所能生产的最大产量。所以，E点是两种要素投入的最优组合点。

等产量线和既定等成本线相切时必定满足：等产量线的斜率与等成本线的斜率相同。由前面的分析已知，等产量线的斜率的绝对值可由边际技术替代率表示，等成本线的斜率的绝对值等于两要素的价格比。因此在E点处一定满足以下条件：

MRTSLK＝ω/r即ΔK/ΔL＝ω/r或MPL/MPK＝ω/r

当然，确定最优要素组合还有另外一种方法，即在既定产量条件下，当所用成本最小时的要素投入量组合就是最优要素投入组合。如图4-5所示，图中显示了三条等成本线GF、AB和CD，其中GF代表的成本投入最低，但在既定的技术条件下利用GF所代表的成本投入是生产不出既定产量Q的；等成本线CD与等产量线Q有两个交点，说明等成本线CD的成本投入是能够生产出产量Q的，但由于它的支出水平过高，理性的生产者会在保持产出水平的基础上逐渐减少成本开支，直到降到等成本线AB所代表的成本为止。由此容易知道，生产既定产量Q时，与既定等产量线相切的等成本线AB所对应的成本为最小成本，其与既定等产量线相切的E点所对应的要素投入组合为最优要素投入组合。

图4-5　最优要素投入组合（二）

（五）扩展线

在其他条件不变时，当产量或成本发生变化时，生产者会重新选择最优要素投入组合，在变化了的产量条件下实现最小成本，或在变化了的成本条件下实现最大产量。扩展线就是研究这方面的问题。

在生产要素价格、技术水平和其他条件不变时，如果生产者改变成本，等成本线就会发生平移；如果生产者改变产量，等产量线也会发生平移。这些不同的等成本线与不同的等产量线相切，形成一系列不同的生产均衡点，这些均衡点的轨迹就是扩展线。如图4-6中，连接E1、E2、E3等均衡点的曲线OS就是一条扩展线。

图4-6　扩展线

扩展线是生产者在长期的扩张或收缩时所遵循的路线。

（六）规模报酬

生产者沿着扩展线改变最优生产要素组合，实际上就是对生产规模的调整。当调整生产规模时就涉及规模报酬问题，规模报酬的变化可以分为规模报酬递增、规模报酬不变和规模报酬递减三种情况。

规模报酬递增是指，产量增加的比例大于生产要素增加的比例。例如，当全部生产要素劳动和资本都增加100%，产量的增加却大于100%，这就是规模报酬递增。引起规模报酬递增的原因是规模经济，即由于企业规模扩大所带来的生产效率的提高。它主要表现在，随着企业规模的扩大，先进的技术和机器设备等生产要素的使用会更普遍；另外，规模扩大也意味着分工更细，而分工能提高生产效率。

规模报酬不变是指，产量增加的比例等于生产要素增加的比例。例如，当劳动和资本同时增加100%，产量也增加100%，这就是规模报酬不变。

规模报酬递减是指，产量增加的比例低于生产要素增加的比例。例如，当劳动和资本同时增加100%时，产量的增加却少于100%，这就是规模报酬递减。引起规模报酬递减的原因是规模不经济，即由于企业规模扩大所带来的生产效率的下降。它主要表现在，当企业规模过大时，会导致管理成本上升、浪费严重等现象发生，从而使生产效率下降。

规模报酬的三种情况可以用图4-7来说明。图4-7中有三张分图，每张分图中都有三条等产量线Q1、Q2、Q3和一条由原点出发的射线形的扩展线OS，图中的等成本线省略。

图4-7（1）表示规模报酬递增，例如由A点到B点，ΔL＝L2－L1，ΔK＝K2－K1，两要素的增加比率为：ΔL/L1＝ΔK/K1＝AB/OA。由图4-7（1）容易看出，两要素增加的比率是小于1的，即小于100%。而由A到B，产量由100增加到200，增加的比率等于100%。显然要素增加的比率是小于产量增加的比率的。在规模报酬递增的情况下有：OA＞AB＞BC。

图4-7（2）表示规模报酬不变，此时由A点到B点，由图示可以看出，要素增加的比率AB/OA是等于100%的（因为AB＝OA），而产量由100增加到200，其增加的比率也是100%，要素增加的比率等于产量增加的比率。在规模报酬不变的情况下有：OA＝AB＝BC。

图4-7（3）表示规模报酬递减，此时由A点到B点，由图示可以看出，要素增加的比率AB/OA是大于100%的（因为AB＞OA），而产量由100增加到200，其增加的比率还是100%，要素增加的比率大于产量增加的比率。在规模报酬递减的情况下有：OA＜AB＜BC。

一般地，在长期生产过程中，企业规模报酬的变化呈现出以下规律：当一开始企业规模较小时，随着规模的扩大会产生规模报酬递增；当规模达到一定程度后，在一定限度内，随着规模扩大会出现一段规模报酬不变阶段，这一阶段被称为企业的适度规模；当超过了适度规模后，如果继续扩大规模，会出现规模报酬递减。企业规模报酬的这种变化规律通常称为规模报酬递减原理。

规模报酬递减原理说明，企业的规模不是越大越好，也不是越小越好，而是有一个适度的规模。因此，在长期生产中，生产者在调整生产规模时，应当把生产规模控制在适度的范围内。

图4-7　规模报酬