（一）消费者均衡的实现

为了考察消费者选择购买物品达到均衡状态必须具备的条件，我们必须假定：一是消费者的偏好既定，即消费者的无差异曲线图为既定；二是消费者的收入M是既定不变的；三是物品x和物品y的价格Px和Py既定不变。

根据消费者预算线和无差异曲线分析可知，在通常情况下收入是相对稳定的，所以消费者预算线只有一条，而无差异曲线可以有无数条。这样，如果把无差异曲线与预算线合在一个平面坐标图上，一条预算线肯定会与无数条无差异曲线中的一条相切。假定有切点E，则消费者按E点上的物品组合来花费其收入，即实现了消费者均衡，该切点就是消费者均衡点。可以用图3-7来说明。

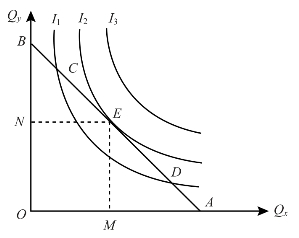
图3-7　消费者均衡

在图3-7中，横轴Qx与纵轴Qy表示物品x和y的数量，I1，I2，I3是3条效用水平不同的无差异曲线，其效用大小的顺序是I1＜I2＜I3，AB是预算线。AB与I2相切于E点，实现了消费者均衡。也就是说，在收入和价格既定的条件下，消费者购买ON数量的x物品，OM数量的y物品，就能获得最大的效用。

为什么只有在E点时才能实现消费者均衡呢？在图3-7中可以看出，I3的效用大于I2，但I3与AB既不相切也不相交，说明达到I3效用水平的x物品与y物品的数量组合在收入和价格既定的条件下是无法实现的。

AB与I1相交于C和D点，在C、D两点上，所购买的x物品和y物品的数量也是收入与价格既定条件下最大的组合，但由于I1＜I2，说明C、D两点上x物品和y物品的组合并不能达到最大效用，它们所实现的效用水平仍然是I1所代表的效用水平。AB线与I2相切于E点，说明按E点进行消费者组合也是现有收入水平所许可的，其实现的是I2所代表的效用水平。由于I2的效用水平大于I1，所以，按E点进行的消费组合的效用水平就必然大于C、D两点的效用水平。此外，由于无数条无差异曲线相互平行，因而能与既定的消费预算线AB相切的无差异曲线只能有一条，而且是距离原点最远的一条，也就是图中的I2。由此可以看出，E点就成为在收入与价格既定条件下的消费者效用最大化的消费组合点，因此，只有在E点才意味着消费者均衡的实现。

在消费者均衡点，即无差异曲线和消费预算线的切点上，消费预算线的斜率与无差异曲线的斜率相等。消费预算线的斜率是两种商品的价格比率，即，无差异曲线的斜率是边际技术替代率，即，这就是说，增加Δx所增加的x物品的效用MUX·Δx等于减少Δy所放弃的y物品效用MUy·Δy。即MUx·Δx＝MUy·Δy。因此，消费者均衡也可以表示为

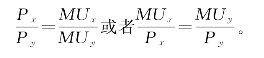
可见，以序数效用论为基础的无差异曲线分析得出的消费者均衡条件，与以基数效用论为基础的边际效用分析得出的消费者均衡条件完全相同，两者的区别只是方法上的不同。

（二）消费者均衡的变动

前面分析了消费者行为时，假设了物品价格、消费者收入、消费者偏好等因素不变，下面分析物品价格和消费者收入变动时对消费者行为的影响。

1．价格变化：价格-消费曲线

在其他条件均保持不变时，一种物品价格的变动会使消费者效用最大化的均衡点的位置发生变动，并由此可以得到价格-消费曲线。假定现有两种物品X1和X2，消费者收入和其中一种物品价格X2的价格不发生变动，价格-需求曲线就是表示在其他条件不变时，价格变动引起的消费者均衡变动的轨迹。具体变动以图3-8来说明。

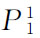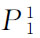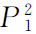在图3-8中，假定物品X1的初始价格为，相应的预算线为AB，它与无差异曲线U1相切于效用最大化的均衡点E1。如果商品X1的价格由下降为，相应的预算线由AB移至AB′，于是，AB′与另一种较高无差异曲线U2相切于均衡点E2。如果商品X1的价格再由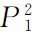继续下降为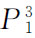，相应的预算线由AB′移至AB″，于是，AB″与另一条更高的无差异曲线U3相切于均衡点E3……不难发现，随着物品X1的价格的不断变化，可以找到无数个诸如E1、E2和E3那样的均衡点，它们的轨迹就是价格-消费曲线。(www.daowen.com)

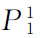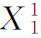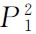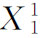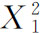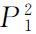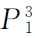分析图3-8（a）中价格-消费曲线上的三个均衡点E1、E2和E3可以看出，在每一个均衡点上，都存在着物品1的价格与物品1的需求量之间一一对应的关系。这就是：在均衡点E1，商品1的价格为，则商品1的需求量为。在均衡点E2，物品1的价格由下降为，则物品1的需求量增加为。在均衡点E3，物品1的价格进一步由下降为，则物品1的需求量由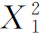再增加为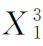。根据物品1的价格和需求量之间的这种对应关系，把每一个P1数值和相应的均衡点上的X1数值绘制在物品的价格-数量坐标图上，便可以得到单个消费者的需求曲线。这便是图3-8（b）中的需求曲线X1＝f（P1）。在图3-8（b）中，横轴表示物品1的数量X1，纵轴表示物品1的价格P1。图（b）中需求曲线X1＝f（P1）上的a、b、c点分别和图3-8（a）中的价格-消费曲线上的均衡点E1、E2、E3相对应。

至此，我们用无差异曲线推导出需求曲线是向右下方倾斜的，它表示物品的价格和需求量呈反方向变动。特别说明的是，需求曲线上与每一价格水平相对应的物品需求量都是可以给消费者带来最大效用的均衡数量。

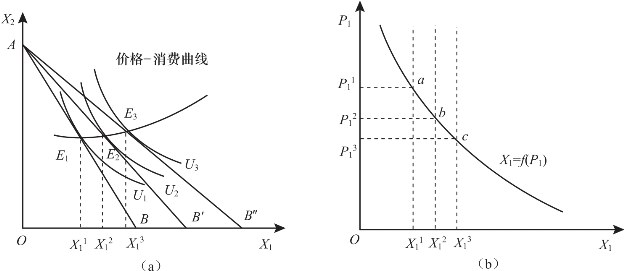
图3-8　价格-消费曲线

2．收入变化：收入-消费曲线

在其他条件均保持不变时，仅有消费者收入水平变动会使消费者效用最大化的均衡点的位置发生变动，并由此可以得到收入-消费曲线。假定物品X1和X2的价格均保持不变，消费者收入发生变动，收入-需求曲线就是表示在其他条件不变时，收入变动引起的消费者均衡变动的轨迹。具体变动以图3-9来说明。

在图3-9（a）中，随着收入水平的不断增加，预算线由AB移至A′B′，再移至A″B″，于是，形成了三个不同收入水平下的消费者效用最大化的均衡点E1、E2和E3。如果收入水平的变化是连续的，则可以得到无数个这样的均衡点的轨迹，这便是图3-9（a）中的收入-消费曲线。图3-9（a）中的收入-消费曲线是向右上方倾斜的，它表示：随着收入水平的增加，消费者对物品1和物品2的需求量都是上升的，所以，图3-9（a）中的两种商品都是正常品。

在图3-9（b）中，采用与图3-9（a）中相类似的方法，随着收入水平的连续增加，描绘出了另一条收入-消费曲线。但是图3-9（b）中的收入-消费曲线是向左上方弯曲的，它表示：随着收入水平的增加，消费者对商品1的需求量开始是增加的，但当收入上升到一定水平之后，消费者对商品1的需求量反而减少了。这说明，在一定的收入水平上，物品1由正常物品变成了劣等品。我们可以在日常经济生活中找到这样的例子。譬如，对某些消费者来说，在收入水平较低时，土豆是正常品；而在收入水平较高时，土豆就有可能成为劣等品。因为，在他们变得较富裕的时候，他们可能会减少对土豆的消费量，而增加对其他食物的消费量。

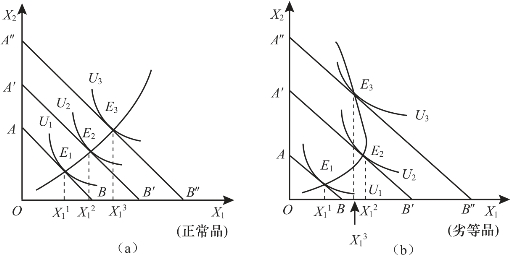
图3-9　收入-消费曲线

3．恩格尔曲线

由消费者的收入-消费曲线可以推导出消费者的恩格尔曲线。以德国19世纪后期统计学家恩格尔的名字命名的恩格尔曲线表示消费者在每一收入水平对某种物品的需求量。与恩格尔曲线相对应的函数关系为x＝f（I）。其中，I为收入水平，x为某种物品的需求量。图3-9中的收入—消费曲线反映了消费者的收入水平和商品的需求量之间存在一一对应关系，对应到图3-10中，曲线就是表示了收入变化和X物品消费量变化，这就是恩格尔曲线。

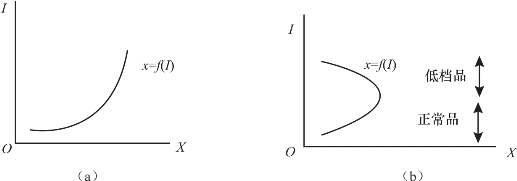
图3-10　恩格尔曲线

图3-10（a）和图3-9（a）是相对应的，图中的X是正常品，X的需求量随着收入水平I的上升而增加，从而使收入-消费曲线和恩格尔曲线向右上方倾斜；而当正常品转变为低档商品时，图形就如3-10（b）所示，低档商品需求随收入的上升而下降，从而使其收入-消费曲线和恩格尔曲线向左上方倾斜。恩格尔在统计研究中发现，随着家庭收入的增加，收入中用于食物的支出占收入的比重越来越小。这种已被上百次研究所证明的理论被称为恩格尔定律。食品支出占家庭收入的比重被称为恩格尔系数。很明显，随着收入的增加，恩格尔系数有降低的趋势。