为了得到可用于计量分析的数据，我们将公式6.1最优城市规模理论模型的生产函数改进：

其中y代表产出，r和j分别代表城市和部门，q（h）表示j产业中间投入品h的投入数量，n表示中间投入品种类的范围，K和L代表资本和劳动力两种生产要素。对比公式6.1和公式6.28，在公式6.1中，中间产品是唯一的生产要素，而标准的经济学生产函数中一般都包括资本和劳动力两种生产要素。因此，公式6.28将这两种要素考虑进来。另外，公式6.28增加了希克斯中间技术进步义。总体上看，公式6.1和公式6.28的基本内涵一致。

因此，整个城市的产出为：

其中Y代表整个城市的产出，X（·）表示一组中间投入品。为了方便计量分析和指标设计，我们把y看作城市的制造业部门，X（·）看作城市的服务业部门，它们按照D-S垄断竞争方式生产，因而具有规模收益递增的特性。

将中间品的生产设定为包含资本和劳动的形式：

因此，整个城市的产出可以进一步表达为：

上式表示的生产过程存在着递增的规模收益，它包含了反应中间产品种类的变量n。如前文所述，城市的集聚经济是通过中间产品种类多样化程度体现的；另外，包含在公式6.31中的最终产品部门（制造业）也符合规模收益递增的特征。

我们使用通勤成本表示城市的聚集不经济。这种不经济主要表现在工人因花费在通勤上的时间，从而放弃的劳动时间。如果N表示整个城市的就业人口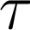，（N）为每个居民扣除通勤成本后的实际劳动力供给，不考虑劳动力参与率，于是有： (www.daowen.com)

从而我们进一步改进城市生产函数为：

上式体现了由于城市规模递增所带来的聚集经济和由于拥挤而导致的通勤成本这种聚集不经济之间的相互制约关系。

综上，可以将公式6.33转换为计量方程。该计量方程有两个关键点：首先，既然不同类型城市由不同的最优规模，那么用什么变量来反映城市类型。Au和Henderson（2004）提出用制造业与服务业增加值的比重作为城市类型划分的依据，因为对大多数国家而言，城市规模等级越高，服务业越发达，在城市经济中所占份额越大，从而，制造业与服务业增加值的比值越低。其次，集聚经济与不经济相互作用而形成的倒U型人均净收益（或净工资）—城市规模曲线关系用什么样的方程式更准确地表示出来，进而得到城市最优规模。这点可以通过人口规模的二次函数即可做到。

根据上面公式的推导，我们把计量方程的形式设定为：

其中，为制造业与服务业增加值的比重，由上式我们可以得到人均净收益最大时的城市人口规模，即最优城市规模：

一般意义上来讲，小于0，这意味着在其他条件不变的情况下，服务业的比重越大，最优城市的规模越大。