基于前面的分析，我们现在可以通过考察城市居民的效用水平与城市人口规模的关系来推导城市最优规模。考虑到城市居民具有相同的收入、消费倾向和效用函数，而且因为交通费用与土地租金相互抵消而形成的空间满意度（Spatial satisfaction）的无差异性，所以，在均衡条件下，城市内所有居民的效用水平都相同。将公式6.25代入城市总生产函数方程，然后除以城市人口N，得到城市居民的人均净收益（或净工资）方程式：

公式6.26显示了城市居民净收益（y）与城市规模（N）、交通成本（τ）、城市聚集经济收益（由ρ反映）这3个变量的关系。在一定条件下，即：

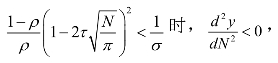这时，y是一个关于N的凹函数，如图6.2所示。令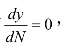容易得到最优城市规模的表达式：

因此，最优城市规模可以看作由城市规模收益递增所带来的聚集经济与因为拥挤成本（通勤成本）导致的聚集不经济两种对立力量相互制衡的结果。最优规模N*随着以τ表示的交通成本的增加而递减，随着以ρ反映的城市总规模收益的增加而递增，从而形成如图6.2所示的倒“U”字形曲线。该曲线与Henderson（1974）、藤田昌久（2005）、Duranton和Puga（2005）等人研究城市规模时推导出的曲线形状相似。起初，随着城市规模增加，城市聚集经济效益占主导地位，人均净收益递增，到达N*点后，城市拥挤成本成为主要因素，城市净收益递减，因此N*点的净收益最大，为最优城市规模点。显然，位于N*左边时，城市规模偏小，反之，则城市规模偏大。

图6.2 人均净收益与城市规模

进一步分析，我们可以得出以下两点基本结论。 (www.daowen.com)

第一，在短期均衡中，城市的均衡规模大于或等于最优规模。如图6.2所示，当均衡规模小于最优规模Ns时，城市因为受到外力的干扰偏离原有的均衡规模，获得人口的城市将越来越靠近最优规模N*，而失去人口的城市偏离最优规模N*越来越远，人口数量会进一步减少，所以，该均衡规模是不稳定的。相反，当均衡规模Nd大于最优规模N*时，城市在偏离原有的均衡状态以后，城市规模会围绕均衡水平上下波动，但波动的幅度越来越小，最后会回复到原来的均衡点。这意味着在人口自由流动的条件下，城市的规模偏大。其主要原因是缺乏有效政策干预，市场失灵导致城市形成机制受阻，新城市难以形成，关于这点，本章后面有详细阐述。

第二，城市只存在一个产业（或最终产品部门），从事完全专业化的生产（参见公式6.17），产业的专业化程度越高，城市的规模越大。图6.3显示了产业1和产业2的倒“U”字形净工资曲线，相对产业1，产业2具有更大的规模经济效应，显然，城市2的最优规模N2*大于城市l的规模N1*。

图6.3 不同类型城市的最优规模

有必要说明的是，城市之所以从事完全专业化生产，与本部分模型的条件假设有关：中间投入品只在部门或产业内流动，而无法在部门或产业间流动，最终产品无运输成本，而中间投入品的运输成本无穷大，因而，城市的聚集经济完全来自于产业内部，表现为地方化经济。