我们假设城市r有m个最终产品部门，部门种类用上标j表示，j=1，……，m。每个部门都对中间投入品有多样化的需求，即中间投入品种类越多，该产业的产出越多。在部门内，中间投入品有很好的相互替代性，但与其他产业的中间投入品之间不存在替代性。假设部门j的生产函数符合不变替代弹性函数（CES）：

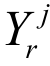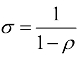其中代表j部门的产出，qj（h）表示j产业每种可得中间投入品h的数量，表示中间投入品种类的范围，参数ρ表示最终产品部门对中间产品的多样化偏好程度，当ρ趋近于1时，中间产品间几乎是完全替代的，当ρ趋近于0时，最终产品部门对更多种类差异化中间产品的需求越来越强。令 则σ表示任意两种中间产品之间的替代弹性。

公式6.1最早由Ethier（1982）提出，它与新经济地理学模型的生产函数非常相似，都是基于迪克西特-斯蒂格利茨的垄断竞争模型框架下的函数形式，但两者针对的集聚机制却是不同的，前者将中间产品的多样化投入需求作为重要的集聚因素来考虑，而后者主要考虑的是消费者的多样化偏好。

假定中间产品的生产具有规模收益递增和垄断竞争的特点，而且所有中间产 品的生产技术都相同，唯一的要素投入是劳动力lj （h），固定投入为αj，劳动力的边际产量为βj，则中间产品的生产函数为：

因为规模收益递增、部门对多样化中间产品的偏好以及存在无限种潜在差异性中间产品的可能，所有厂家都会选取生产与其他厂商不同的产品，即每种产品只能在一个生产部门由一个专业化厂商生产，所以厂商的数目与多样性的中间产品种类相同。

假定中间产品的价格为pj（h），为了使最终产品的成本最低，需要以公式6.1为约束条件，求解 的最小值，即

公式6.3的一阶条件是边际替代率等于价格比值，即

显然有：

将公式6.5代入约束条件得：

每个厂商实现自身利润最大化的条件是边际成本等于边际收益。公式6.6表明，每个厂商的需求价格弹性为因此厂商的边际收益为。用ωj（因为每个变量对应的都是相同的中间产品h，为了等式的简练，以下各变量不再标示参数h）表示劳动力工资，由公式6.2可知，厂商的边际成本为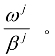所以，对每个进入厂商而言下式立：

亦即：

城市j部门的利润可表示为：

将公式6.2和公式6.8代入公式6.9可得： (www.daowen.com)

前面已指出，每个厂商生产一种商品，自由进入市场并且追求最大化利润，所以只要市场上还存在着超额利润，就会有新的厂商（即新的产品）进入。由于部门内的中间产品的替代弹性相同，新产品的加入必将降低部门内已有产品的需求，导致利润下降，直到最后一个进入厂商的超额利润为零，市场处于均衡状态。该市场均衡类似于零超额利润条件下的张伯伦垄断竞争（1933）均衡。

零利润条件下，自由进出厂商的均衡产出为：

相应的均衡劳动力投入为：

如果Lj 表示j部门的所有劳动力数量，nj表示j部门的厂商数目，那么有：

将公式6.11和公式6.13代入公式6.1，则r城市j部门的生产函数可表示为：

令 为大于零的常数，公式6.14变为：

从公式6.13和公式6.15可以看出，所有最终产品部门的规模效应都是通过中间产品种类多样化程度体现出来的，中间产品种类越多，最终产品部门的产出越大。

最开始，我们假定的是城市存在m个最终产品部门，那么，在市场均衡的条件下，这些部门能否在一个城市中并存呢？零超额利润条件意味着最终产品部门应满足：

为r城市j部门的最终产品价格。将公式6.15代入公式6.16可得：

因为劳动力可以在城市各部门间流动，所以市场均衡条件下，各部门的工资水平是相等的。假设由于偶然原因，市场出现某种扰动，有一小部分劳动力从一个部门流向另一个部门。公式6.17显示，劳动力流入的部门，因为拥有了更多样的中间产品供给，而具备更高的产出水平，进而提高工资水平，工资率上升又将进一步吸引更多的劳动力流入。相反，劳动力沆出部门，工资率会越来越低，进而流失更多的劳动力。因此，最终的市场均衡结果是每个城市只存在一个最终产品部门，从事完全专业化的生产。

基于以上分析，公式6.15中的上标j可以省略，r城市的总生产函数变为：