本节选用多项式Logit模型描述托运人的选择行为，这也是市场营销学领域常用的一类模型[152-154]。在MNL模型框架下，托运人基于运价的比较决定是否订舱，他独立行动，力求实现自身效用的最大化。

本节所涉及的相关变量主要包括：

N：特定航段上参与市场竞争的班轮公司总数；

i：所涉班轮公司的序号，i=1，2，…，N；

D：特定航次销售期的长度，单位为“日”；

t：销售期中每一天的序号，首日为1，最后一日为D；

Πi：班轮公司i在整个销售期的期望总收益；

S i：班轮公司i的运力，即船上的箱位数；

p i（t）：班轮公司i在第t日所设定的运价；

P i：向量（p i（1），p i（2），…，p i（D）），即班轮公司i在整个销售期差别定价方案；

p（t）：向量（p 1（t），p 2（t），…，p n（t）），即所有班轮公司在第t日设定的运价；

λ（t）：托运人在第t日的到达率，即第t日的托运人数量；

αi：表征班轮公司i的服务质量、品牌形象、受欢迎度等的参数；

β：表征托运人价格反应的参数；

μ：转移参数（shift parameter）；

η：规模参数（scale parameter）。

其中，P i为决策变量，具体则由p（t）i构成。

本节建模还基于以下假设：

（1）所有班轮公司均为理性市场参与者。

（2）每家班轮公司每日可调整一次运价。

（3）N，i，D，t，Si，λ（t），αi，β，μ及η为公开信息。

（4）针对特定航次，所有班轮公司的销售期一致。

（5）每家班轮公司均不知晓其竞争对手的实时销售进展。

（6）每家班轮公司在特定销售期中不能补充运力，未售出的箱位在销售期届满后不具有残值。(www.daowen.com)

（7）单个托运人每次预订一个箱位以适用多项式Logit模型，若某个托运人单次预订多个箱位，则将视为相应个数的托运人。

对于每个托运人，其从班轮公司i订舱后所得到效用为[152]

其不订舱所获得的效用为

式中，Z i是相互独立的随机变量，以描述每位托运人的个性偏好，服从以下形式的Gumbel分布：

托运人面对第t日所有班轮公司的报价，即p（t）时，将以其效用最大为目标进行选择，他向班轮公司i订舱的概率为[155]

不订舱的概率为

在销售期的不同时段订舱的托运人往往对价格有不同的敏感性。可以在航空客运中找到一个类似的例子：对价格更为敏感的出行人群通常会于出行前提早很长时间订座，以获得更为优惠的折扣，而商务旅客的价格敏感度则相对较低，根据出行的实际需要随时订座，有时甚至是即时订座。这一现象在动态定价研究中时常被忽略，很明显，应将托运人的价格反应参数与时间关联，即将β进一步细化为β（t）。因此，式（6-43）和式（6-44）可进一步表达为

和

由于参数μ和η可被并入到αi和β（t）中去，在计算ρi（t）（p（t））时，可令μ=0、η=1，这是解决这一问题的一个常用技巧，且不失一般性。由式（6-45）可知，对于运价单调递减，同时有

因此，如果一家班轮公司不愿向某一托运人提供箱位，他就可以将运价设定在一个极高的水平（理论上为正无穷），该条件下，其期望收益也就为0。此外，如果一家班轮公司在销售期结束前所有箱位就已售罄，对于托运人及其他班轮公司而言，该班轮公司在剩余的销售期中将其运价设置为无穷大。每家班轮公司差异化设置各自销售期每天的运价，从而使得能在整个销售期间获得最大的收益。班轮公司i的目标函数可以表达为

考虑到单个航次运力的限制，相应的约束条件也不可或缺：

当然，班轮公司i每日设定的运价还应该是非负的，即

根据Kinderlehrer等（1980）[156]及Nagurney（1999）[157]的研究，若Φb为有界、凸、闭集，F（X）连续，则变分不等式＜F（X b），X-X b≥0，∀X b∈Φb至少存在一解。

对于班轮公司i，相应的优化拉格朗日函数为

其对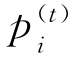和γi的偏导分别为

在式（6-52）中，

相应的变分不等式可以表达为

因此，不失一般性，对于本节的博弈模型，当ζi≥0且εi≥0，Φb={p 1（t），…，p N（t）；γ1，…，γN}，p i（t）∈[0，ζi]，γi∈[0，εi]。

在此假设下，Φb显然是一个有界、凸、闭集，基于式（6-54），向量函数可以表达为

由式（6-55）可知，对于{p 1（t），…，p N（t）；γ1，…，γN}，F（X）显然是连续的。

综上所述，由本节博弈模型推导的变分不等式满足文献[156]、[157]的条件，因此，该博弈存在至少一个纯策略纳什均衡。

相似博弈模型均衡的存在性与唯一性证明也可参考文献[158]。